题目内容
一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长是:
A. | B. | C.2 | D.3 |
D
解析试题分析:连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边高的 倍.题目中一个边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
倍.题目中一个边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为 ,即OC=
,即OC= ,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
连接OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4,
∴高为2 ,即OC=
,即OC= ,
,
∵∠ACB=60°,故有∠OCF=30°,
∴在Rt△OFC中,可得FC= ,
,
∴CE=3.
考点:切线的性质,等边三角形的性质,解直角三角形,垂径定理
点评:本题知识点多,中考性强,在中考中比较常见,一般出现在选择、填空的最后一题,难度较大.

练习册系列答案
相关题目
 如图,小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则该圆的半径为( )
如图,小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则该圆的半径为( )A、3
| ||
B、3
| ||
C、4
| ||
D、4
|

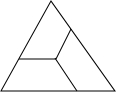 如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为
如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为