题目内容
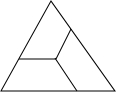 如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为
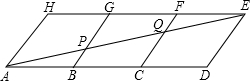
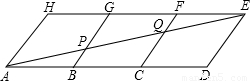
如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为分析:根据等边三角形的性质和等腰梯形的性质推出△DCF和△ADF是等边三角形,推出AD=DF=AF,DC=CF=DF,根据平行四边形的性质推出AD=DC=FC=BF,代入求出即可.
解答: 解:延长ED交BC于F,
解:延长ED交BC于F,
∵用三个全等的等腰梯形拼接成一个边长为a的等边三角形,
∴∠B=∠DCB=∠EFC=60°,
∴DC=DF,
∴△DFC是等边三角形,
∴DF=FC=DC=AB,∠FDC=60°,
∵AD∥BC,
∴∠ADF=60°,
∵AD∥BC,DE∥AB,
∴四边形ADFB是平行四边形,
∴AD=BF,AD=BF,
同理AF=DC,
∴AF=DF,
∴△ADF是等边三角形,
∴AD=DC=FC=BF,
∴BF=CF=CQ=
,
故答案为:
.
 解:延长ED交BC于F,
解:延长ED交BC于F,∵用三个全等的等腰梯形拼接成一个边长为a的等边三角形,
∴∠B=∠DCB=∠EFC=60°,
∴DC=DF,
∴△DFC是等边三角形,
∴DF=FC=DC=AB,∠FDC=60°,
∵AD∥BC,
∴∠ADF=60°,
∵AD∥BC,DE∥AB,
∴四边形ADFB是平行四边形,
∴AD=BF,AD=BF,
同理AF=DC,
∴AF=DF,
∴△ADF是等边三角形,
∴AD=DC=FC=BF,
∴BF=CF=CQ=
| a |
| 3 |
故答案为:
| a |
| 3 |
点评:本题主要考查对等腰梯形的性质,平行四边形的性质和判定,等边三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目