题目内容
20．已知点A（2，a），B（-b，4），分别根据下列条件求a，b的值．（1）若点A，B关于y轴对称，则a=4，b=2；
（2）若点A，B关于x轴对称，则a=-4，b=-2．
分析 结合关于x轴、y轴对称的点的坐标的特点：（1）关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，-y）；（2）关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．即点P（x，y）关于y轴的对称点P′的坐标是（-x，y）．求解即可．
解答 解：（1）若点A，B关于y轴对称，
则a=4，
-b=-2，b=2，；
（2）若点A，B关于x轴对称，
则a=-4，
-b=2，b=-2．
故答案为：（1）4，2，（2）-4，-2．
点评 本题考查了关于x轴、y轴对称的点的坐标，解答本题的关键在于熟练掌握：（1）关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，-y）；（2）关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．即点P（x，y）关于y轴的对称点P′的坐标是（-x，y）．
练习册系列答案
小夫子全能检测系列答案
相关题目
如图．在△ABC中，△ABC的高AD、CE相交于点H，∠B=57°，则∠AHC=123°度．
8．
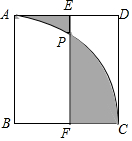如图，在边长为2的正方形ABCD中，以B点为圆心，AB为半径构造扇形ABC，点P是AC上一动点，过P作EF⊥BC，分别交AD、BC于E、F．记AE、PE、$\widehat{AP}$构成的封闭区域为S1，PF、FC、$\widehat{PC}$构成的封闭区域为S2，当S1与S2面积相等时，BF的长为（ ）
如图，在边长为2的正方形ABCD中，以B点为圆心，AB为半径构造扇形ABC，点P是AC上一动点，过P作EF⊥BC，分别交AD、BC于E、F．记AE、PE、$\widehat{AP}$构成的封闭区域为S1，PF、FC、$\widehat{PC}$构成的封闭区域为S2，当S1与S2面积相等时，BF的长为（ ）| A． | 1 | B． | $\frac{4}{3}$ | C． | $\sqrt{2}$ | D． | $\frac{π}{2}$ |