题目内容
13.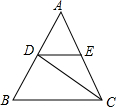 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
分析 根据等边三角形的性质可得AD=$\frac{1}{2}$AB,然后判断出△ADE和△ABC相似,根据相似三角形周长的比等于相似比求解即可.
解答 解:∵CD是∠ACB的平分线,△ABC是等边三角形,
∴AD=$\frac{1}{2}$AB,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{△ADE的周长}{△ABC的周长}=\frac{AD}{AB}$,
∵△ABC的边长为a,
∴△ABC的周长为3a,
∴$\frac{△ADE的周长}{3a}=\frac{1}{2}$,
解得△ADE的周长=1.5a.
故选C
点评 本题考查了等边三角形的性质,相似三角形的判定与性质,等边三角形是特殊的等腰三角形,也符合三线合一的性质,作出图形更形象直观.

练习册系列答案
相关题目
3.“十二五”期间,将新建保障性住房约37000000套,用于解决中低收入和新参加工作的大学生住房的需求,把37000000用科学记数法表示应是( )
| A. | 37×106 | B. | 3.7×106 | C. | 3.7×107 | D. | 0.37×108 |
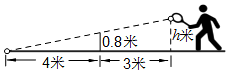 如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为1.4米.
如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为1.4米.
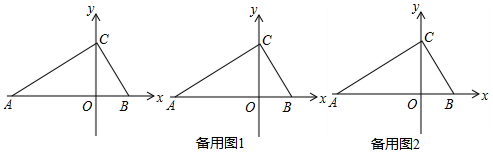
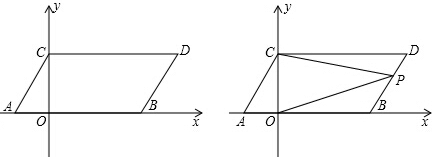
 如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD
如图,在平面直角坐标系中,点C在y轴上,点A(a,0)、点B(a-4,0),位于原点两侧,且∠ABC=60°,AE⊥BC,交y轴于点F,交BC于点E,点D在点B的左侧,且∠CDO=45°,AB=2BD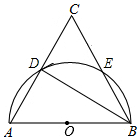 如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,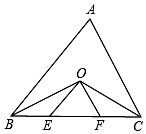 如图,△ABC中,∠ABC、∠ACB的平分线BO、CO相交于点O,OE∥AB,OF∥AC,△OEF的周长=10,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线BO、CO相交于点O,OE∥AB,OF∥AC,△OEF的周长=10,则BC的长为( )