题目内容
2.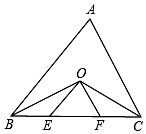 如图,△ABC中,∠ABC、∠ACB的平分线BO、CO相交于点O,OE∥AB,OF∥AC,△OEF的周长=10,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线BO、CO相交于点O,OE∥AB,OF∥AC,△OEF的周长=10,则BC的长为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
分析 由OB,OC分别是△ABC的∠ABC和∠ACB的平分线和OE∥AB、OF∥AC可推出BE=OE,OF=FC,显然△OEF的周长即为BC的长度
解答 解:∵OB,OC分别是∠ABC,∠ACB的平分线,
∴∠ABO=∠EBO,∠ACO=∠FCO,
∵OE∥AB,OF∥AC,
∴∠ABO=∠BOE,∠ACO=∠COF,
∴∠EBO=∠BOE,∠FCO=∠COF,
∴BE=OE,OF=FC,
∴BC=BE+EF+FC=OF+OE+EF,
∵△OEF的周长=10,
∴OF+OE+EF=10
∴BC=10.
故选B.
点评 此题运用了平行线性质,角平分线定义以及等腰三角形的判定定理,较为灵活,难度中等.

练习册系列答案
相关题目
13.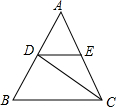 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
10.己知实数m,n满足3m2+6m-7=0,3n2+6n-7=0,且m≠n,则$\frac{1}{m}$$+\frac{1}{n}$=( )
| A. | $\frac{6}{7}$ | B. | -3 | C. | 3 | D. | 7 |
7.如图,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )


| A. | SSS | B. | SAS | C. | AAS | D. | ASA |
14.下列命题中,属于真命题的是( )
| A. | 圆周角等于圆心角的一半 | |
| B. | 在同一圆中,等弧所对的圆周角相等 | |
| C. | 平分弦的直线垂直于弦 | |
| D. | 过弦的中点的直线必经过圆心 |
11.将一块直角三角尺绕它的一条直角边旋转一周,所形成的几何体是( )
| A. | 圆锥 | B. | 三棱锥 | C. | 圆柱 | D. | 三棱柱 |
12.计算:(-1)2015+($\frac{1}{2}$-$\frac{3}{2}$)2016-($\frac{1}{2}$)3的结果为( )
| A. | -$\frac{1}{8}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{6}$ | D. | $\frac{3}{2}$ |
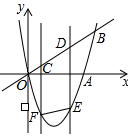 如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.
如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.