题目内容
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是考点:规律型:点的坐标
专题:规律型
分析:根据每一个正方形有4个顶点可知每4个点为一个循环组依次循环,用55除以4,根据上和余数判断出点A55所在的正方形以及所在的象限,再根据正方形的性质写出即可.
解答:解:∵每个正方形都有4个顶点,
∴每4个点为一个循环组依次循环,
∵55÷4=13余3,
∴点A55是第14个正方形的第3个顶点,在第一象限,
∵从内到外正方形的边长依次为2,4,6,8,…,
∴A3(1,1),A7(2,2),A11(3,3),…,A55(14,14).
故答案为:(14,14).
∴每4个点为一个循环组依次循环,
∵55÷4=13余3,
∴点A55是第14个正方形的第3个顶点,在第一象限,
∵从内到外正方形的边长依次为2,4,6,8,…,
∴A3(1,1),A7(2,2),A11(3,3),…,A55(14,14).
故答案为:(14,14).
点评:本题是对点的坐标变化规律的考查,根据四个点为一个循环组求出点A55所在的正方形和所在的象限是解题的关键.

练习册系列答案
相关题目
菱形ABCD中,有一个角为120°,较长的对角线长为4
,则菱形的面积为( )
| 3 |
A、8
| ||
B、12
| ||
C、16
| ||
D、32
|
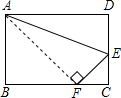 如图,折叠矩形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,则FC=
如图,折叠矩形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,则FC= 如图,在△ABC中,AB=3cm,AC=4cm,BC=5cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E.线段DE的最小值是
如图,在△ABC中,AB=3cm,AC=4cm,BC=5cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E.线段DE的最小值是