题目内容
12.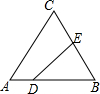 如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )
如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )| A. | 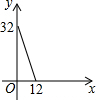 | B. | 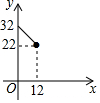 | C. | 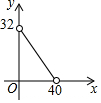 | D. |  |
分析 过点C作CF⊥AB于F,利用相似三角形的性质可得出BE=$\frac{3}{5}$x、DE=$\frac{4}{5}$x,进而可得出y=C△ABC-BD-BE+DE=32-$\frac{4}{5}$x,结合x的取值范围可得出y的取值范围,再对照四个选项中的函数图象,即可得出结论.
解答 解:过点C作CF⊥AB于F,如图所示.
∵AC=BC=10,AB=12,
∴BF=$\frac{1}{2}$AB=6,
∴CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=8.
∵CF⊥AB,DE⊥BC,
∴∠BFC=∠BED,
∴△BFC∽△BED,
∴$\frac{BE}{BF}$=$\frac{DE}{CF}$=$\frac{BD}{BC}$,
∴BE=$\frac{3}{5}$x,DE=$\frac{4}{5}$x,
∴y=C△ABC-BD-BE+DE=10+10+12-x-$\frac{3}{5}$x+$\frac{4}{5}$x=32-$\frac{4}{5}$x.
∵0<x<12,
∴22.4<y<32.
故选D.
点评 本题考查了动点问题的函数图象、相似三角形的判定与性质以及三角形的周长,利用相似三角形的性质结合三角形的周长找出y=32-$\frac{4}{5}$x是解题的关键.

练习册系列答案
相关题目
2. 关于x的不等式x-a≥-2的解集如图所示,则a的值等于( )
关于x的不等式x-a≥-2的解集如图所示,则a的值等于( )
 关于x的不等式x-a≥-2的解集如图所示,则a的值等于( )
关于x的不等式x-a≥-2的解集如图所示,则a的值等于( )| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
3.如果抛物线y=-x2+bx与x轴交于A、B两点,且顶点为C,那么当∠ACB=120°,b的值是( )
| A. | ±$\frac{2\sqrt{3}}{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
20.下列语句写成式子正确的是( )
| A. | 4是16的平方根,即$\sqrt{16}$=4 | B. | 4是(-4)2的算术平方根,即$\sqrt{(-4)^2}$=4 | ||
| C. | ±4是16的平方根,即±$\sqrt{16}$=4 | D. | ±4是16的平方根,即$\sqrt{16}$=±4 |
7.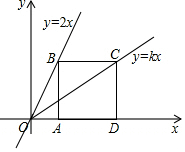 如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
 如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
4.下列命题中正确的为( )
| A. | 相等的圆心角所对的弦相等 | B. | 长度相等的弧是等弧 | ||
| C. | 等弧所对圆周角相等 | D. | 等弦所对圆周角相等 |
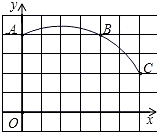 如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,已知点D为x正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为(7,0).
如图,直角坐标系中一条圆弧经过A(0,4),B(4,4),C(6,2)三个网格点,已知点D为x正半轴上的一点,若直线CD与该圆弧相切,则点D的坐标为(7,0).