题目内容
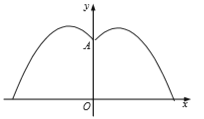
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
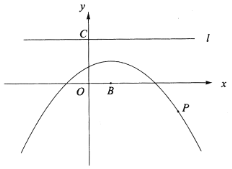
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
【答案】(1)开口方向向下,点A的坐标是![]() ,在对称轴直线
,在对称轴直线![]() 左侧部分是上升的,右侧部分是下降的;(2)点B的坐标为
左侧部分是上升的,右侧部分是下降的;(2)点B的坐标为![]()
【解析】
(1)先化为顶点式,然后由二次函数的性质可求解;
(2)如图,设直线![]() 与对称轴交于点
与对称轴交于点![]() ,则
,则![]() ,设线段
,设线段![]() 的长为
的长为![]() ,则
,则![]() ,可求点
,可求点![]() 坐标,代入解析式可求
坐标,代入解析式可求![]() 的值,即可求点
的值,即可求点![]() 坐标.
坐标.
解:(1)抛物线![]() 的开口方向向下,
的开口方向向下,
顶点![]() 的坐标是
的坐标是![]() ,
,
抛物线的变化情况是:在对称轴直线![]() 左侧部分是上升的,右侧部分是下降的;
左侧部分是上升的,右侧部分是下降的;
(2)如图,设直线![]() 与对称轴交于点
与对称轴交于点![]() ,则
,则![]() .
.
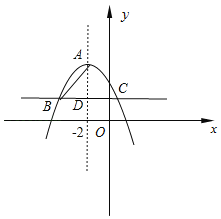
设线段![]() 的长为
的长为![]() ,则
,则![]() ,
,
![]() 点
点![]() 的坐标可表示为
的坐标可表示为![]() ,
,
代入![]() ,得
,得![]() .
.
解得![]() (舍
(舍![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目