题目内容
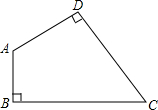 如图所示,在四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=4
如图所示,在四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=4| 3 |
考点:勾股定理
专题:
分析:要想求得四边形ABCD的面积,必须加以辅助线使四边形变成可以求得面积的图形,根据图形特点和已知条件,可以延长BA、CD相交于E,然后求出即可.
解答: 解:延长BA、CD相交于E,
解:延长BA、CD相交于E,
∵∠A=135°,∠B=∠D=90°
∴∠C=360°-90°-90°-135°=45°,
∴△BCE和△ADE都是等腰直角三角形.
S四边形ABCD=S△BCE-S△ADE
=
×4
×4
-
×4×4
=24-8
=16.
故答案为:16.
 解:延长BA、CD相交于E,
解:延长BA、CD相交于E,∵∠A=135°,∠B=∠D=90°
∴∠C=360°-90°-90°-135°=45°,
∴△BCE和△ADE都是等腰直角三角形.
S四边形ABCD=S△BCE-S△ADE
=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
=24-8
=16.
故答案为:16.
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
下列计算正确的是( )
A、3
| ||||||||||||
B、(
| ||||||||||||
C、
| ||||||||||||
D、
|
如果x2与-2y2的和为m,1+y2与-2x2的差为n,那么2m-4n化简后应为( )
| A、-6x2-8y2-4 |
| B、10x2-8y2-4 |
| C、-6x2-8y2+4 |
| D、10x2-8y2+4 |



