题目内容
14．化简：$\sqrt{（-5）^{2}}$=5；$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$．分析 根据算术平方根的定义以及分数的基本性质即可求解．
解答 解：$\sqrt{（-5）^{2}}$=5；
$\frac{6}{\sqrt{2}}$=$\frac{6\sqrt{2}}{2}$=3$\sqrt{2}$．
故答案是：5，3$\sqrt{2}$．
点评 本题考查了算术平方根的定义以及二次根式的化简，二次根式化简的依据是算术平方根的性质和分数的基本性质．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
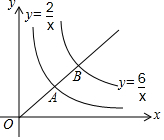在同一坐标系中，反比例函数y=$\frac{2}{x}$和y=$\frac{6}{x}$分别与一个正比例函数在第一象限相交于A、B两点，则OA：OB=$\sqrt{3}$：3．
如图，△ABC≌△ADE，∠B=25°，则∠D=25°．
如图，已知四边形ABCD及点P，画出四边形ABCD关于点P的对称图形A′B′C′D′．
3．观察下面三行数：
（1）a=-27，b=-27，c=-26（提醒：填c时观察③与①有什么关系）
（2）O=（-3）n，P=$（-3）^{n}（-\frac{1}{3}）$，Q=（-3）n+1（提醒：填Q时观察③与①有什么关系）
（3）设x，y，z分别为第①②③行的2016个数，求x+6y+z的值．
| 第n个 | |||||
| -3 | 9 | a | 81 | … | O |
| 1 | -3 | 9 | b | … | P |
| -2 | 10 | c | 82 | … | Q |
（2）O=（-3）n，P=$（-3）^{n}（-\frac{1}{3}）$，Q=（-3）n+1（提醒：填Q时观察③与①有什么关系）
（3）设x，y，z分别为第①②③行的2016个数，求x+6y+z的值．