题目内容
7. 如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的线段是CD、EF.
如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的线段是CD、EF.
分析 由小正方形的面积得出小正方形的边长,由勾股定理求出AB、CD、EF、GH,即可得出结果.
解答 解:∵每个小正方形的面积为2,
∴每个小正方形的边长为$\sqrt{2}$,
∴AB=2$\sqrt{2}$,CD=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,EF=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,GH=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,
∴四条线段中长度是有理数的线段是CD、EF;
故答案为:CD、EF.
点评 本题考查了正方形的性质、勾股定理、实数、有理数;熟练掌握正方形的性质和勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
15.下列说法中,正确的是( )
| A. | 单项式-$\frac{2{x}^{2}y}{5}$的系数是-2,次数是3 | |
| B. | 单项式a的系数为0,次数是3 | |
| C. | 24ab2c的系数是2,次数为8 | |
| D. | 一个n次多项式(n为正整数),它的每一项的次数都不大于n |
2.函数y=$\frac{{{x^2}-6x}}{{{x^2}+2x+1}}$有( )
| A. | 最大值$\frac{9}{7}$ | B. | 最大值$-\frac{9}{7}$ | C. | 最小值$\frac{9}{7}$ | D. | 最小值$-\frac{9}{7}$ |
19.若某数的平方根为2a+3和a-15,则这个数是( )
| A. | -18 | B. | $-\frac{2}{3}$ | C. | 121 | D. | 以上结论都不是 |
17.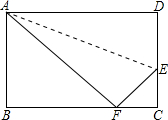 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |