题目内容
 如图,正方形ABCD的外接圆为⊙O,点P在劣弧
如图,正方形ABCD的外接圆为⊙O,点P在劣弧 |
| CD |
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
考点:正多边形和圆
专题:
分析:(1)连接OB,OC,由正方形的性质知,△BOC是等腰直角三角形,根据∠BOC=90°,由圆周角定理可以求出;
(2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
(2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
解答: 解:(1)连接OB,OC,
解:(1)连接OB,OC,
∵四边形ABCD为正方形,
∴∠BOC=90°,
∴∠P=
∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=
=
=4
∴BC=2BE=2×4
=8
.
 解:(1)连接OB,OC,
解:(1)连接OB,OC,∵四边形ABCD为正方形,
∴∠BOC=90°,
∴∠P=
| 1 |
| 2 |
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=
|
|
| 2 |
∴BC=2BE=2×4
| 2 |
| 2 |
点评:本题考查的是圆周角定理、垂径定理及勾股定理,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 若AB∥CD,∠AEH=130°,那么∠EHC等于多少度( )
若AB∥CD,∠AEH=130°,那么∠EHC等于多少度( )| A、60° | B、70° |
| C、65° | D、50° |
 如图,已知∠AOB=α,∠AOC=β,∠BOD=γ,则∠COD的大小为( )
如图,已知∠AOB=α,∠AOC=β,∠BOD=γ,则∠COD的大小为( )| A、α-β-γ |
| B、α+β-γ |
| C、α+γ-β |
| D、β+γ-α |
已知正三角形的周长是6,则该正三角形外接圆的半径是( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知圆锥的底面半径为2cm,母线长为6cm,则圆锥的侧面积是( )
| A、24cm2 |
| B、24πcm2 |
| C、12cm2 |
| D、12πcm2 |
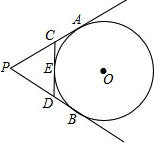 PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是
PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是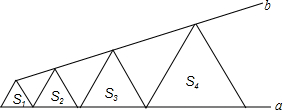 如图,若干个正三角形的一边在同一条直线a上,这边对的顶点也在同一条直线b上,它们的面积依次为S1,S2,S3,S4…若S1=1,S2=2,则S6等于( )
如图,若干个正三角形的一边在同一条直线a上,这边对的顶点也在同一条直线b上,它们的面积依次为S1,S2,S3,S4…若S1=1,S2=2,则S6等于( ) 同学们,你认识如图所示的卡通人物吗?没错,它就是美国著名3D卡通电影《里约大冒险》(Rio)中的主人公,两只漂亮的鹦鹉--布鲁和珠儿,凭借着影片所寄寓的独特情感,该片在2011年3月、4月和5月蝉联全球票房冠军,累计票房达2.86亿美元.“2.86亿”用科学记数法应书写为
同学们,你认识如图所示的卡通人物吗?没错,它就是美国著名3D卡通电影《里约大冒险》(Rio)中的主人公,两只漂亮的鹦鹉--布鲁和珠儿,凭借着影片所寄寓的独特情感,该片在2011年3月、4月和5月蝉联全球票房冠军,累计票房达2.86亿美元.“2.86亿”用科学记数法应书写为