题目内容
 如图,已知∠AOB=α,∠AOC=β,∠BOD=γ,则∠COD的大小为( )
如图,已知∠AOB=α,∠AOC=β,∠BOD=γ,则∠COD的大小为( )| A、α-β-γ |
| B、α+β-γ |
| C、α+γ-β |
| D、β+γ-α |
考点:角的计算
专题:
分析:由∠BOC=∠AOB-∠AOC,可得∠BOC=α-β,又因为∠COD=∠BOD-∠BOC,所以可得∠COD=γ-(α-β)=γ-α+β.
解答:解:∵∠BOC=∠AOB-∠AOC,∠AOB=α,∠AOC=β,
∴∠BOC=α-β,
∵∠COD=∠BOD-∠BOC,∠BOD=γ,
∴∠COD=γ-(α-β)=γ-α+β=β+γ-α.
故选D.
∴∠BOC=α-β,
∵∠COD=∠BOD-∠BOC,∠BOD=γ,
∴∠COD=γ-(α-β)=γ-α+β=β+γ-α.
故选D.
点评:此题考查了角的计算,解题关键是:利用图形用含α、β、γ,表示∠BOC,∠COD.

练习册系列答案
相关题目
在平面直角坐标系内,点P(m-3,m-5)在第三象限,则m的取值范围是( )
| A、m<5 | B、3<m<5 |
| C、m<3 | D、m<-3 |
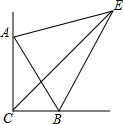 如图,在Rt△ABC中,∠C=90°,∠A=40°,∠C的平分线与∠ABC相邻的外角平分线交于E点,连接AE,则∠AEB等于( )
如图,在Rt△ABC中,∠C=90°,∠A=40°,∠C的平分线与∠ABC相邻的外角平分线交于E点,连接AE,则∠AEB等于( )| A、50° | B、45° |
| C、40° | D、35° |
 如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )cm3.
如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )cm3.| A、2 | B、4 | C、6 | D、8 |
 如图,已知点O是△ABC的外心,弦CM⊥AB,CN是直径,点F是
如图,已知点O是△ABC的外心,弦CM⊥AB,CN是直径,点F是
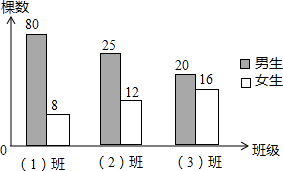 为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是
为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是 如图,正方形ABCD的外接圆为⊙O,点P在劣弧
如图,正方形ABCD的外接圆为⊙O,点P在劣弧 若函数y=-x2+2x+k的部分图象如图所示,由图可知,关于x的方程-x2+2x+k=0的一根是3,则另一根为
若函数y=-x2+2x+k的部分图象如图所示,由图可知,关于x的方程-x2+2x+k=0的一根是3,则另一根为