题目内容
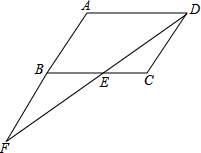 已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.
已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.(1)证明:△DCE≌△FBE;
(2)若EC=3,求AD的长.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)利用平行线的性质得出∠FBE=∠C,进而利用全等三角形的判定定理得出即可;
(2)利用全等三角形的性质结合平行四边形的性质求出即可.
(2)利用全等三角形的性质结合平行四边形的性质求出即可.
解答: (1)证明:∵AB∥CD,
(1)证明:∵AB∥CD,
∴∠FBE=∠C,
∵AB=DC,AB=BF,
∴BF=DC,
在△DCE和△FBE中,
,
∴△DCE≌△FBE(AAS);
(2)解:∵△DCE≌△FBE,
∴BE=EC=3,
∴AD=BC=6.
 (1)证明:∵AB∥CD,
(1)证明:∵AB∥CD,∴∠FBE=∠C,
∵AB=DC,AB=BF,
∴BF=DC,
在△DCE和△FBE中,
|
∴△DCE≌△FBE(AAS);
(2)解:∵△DCE≌△FBE,
∴BE=EC=3,
∴AD=BC=6.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,正确掌握全等三角形的判定与性质是解题关键.

练习册系列答案
相关题目
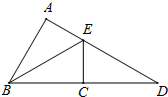 如图,B、C、D在同一直线上,△BAE≌△BCE,△BAE≌△DCE,则∠D=
如图,B、C、D在同一直线上,△BAE≌△BCE,△BAE≌△DCE,则∠D= 如图,⊙O中,OA⊥BC,∠AOB=52°,则∠ADC的度数为
如图,⊙O中,OA⊥BC,∠AOB=52°,则∠ADC的度数为