题目内容
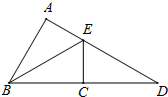 如图,B、C、D在同一直线上,△BAE≌△BCE,△BAE≌△DCE,则∠D=
如图,B、C、D在同一直线上,△BAE≌△BCE,△BAE≌△DCE,则∠D=考点:全等三角形的性质
专题:
分析:由三角形全等的性质可得到∠A=90°,∠ABE=∠EBC=∠D,结合三角形内角和定理可求得∠D.
解答:解:∵△BAE≌△BCE,△BAE≌△DCE,
∴∠A=∠ECB=∠ECD,∠ABE=∠CBE=∠D,
又∵B、C、D在同一直线上,
∴∠ECB+∠ECD=180°,
∴∠A=∠ECB=∠ECD=90°,
∴∠ABE+∠CBE+∠D=90°,
∴3∠D=90°,
∴∠D=30°.
故答案为:30.
∴∠A=∠ECB=∠ECD,∠ABE=∠CBE=∠D,
又∵B、C、D在同一直线上,
∴∠ECB+∠ECD=180°,
∴∠A=∠ECB=∠ECD=90°,
∴∠ABE+∠CBE+∠D=90°,
∴3∠D=90°,
∴∠D=30°.
故答案为:30.
点评:本题主要考查全等三角形的性质,掌握全等三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
计算:(-1)2015等于( )
| A、-2015 | B、2015 |
| C、-1 | D、1 |
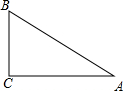 如图,在直角△ABC中,∠C=90°,BC=1,AC=
如图,在直角△ABC中,∠C=90°,BC=1,AC=| 2 |
| A、∠A=90° | ||||
| B、∠A=45° | ||||
C、cotA=
| ||||
D、tanA=
|
 如图所示,等腰△ABC的底角为30°,腰长为12,则底边上的高AD等于
如图所示,等腰△ABC的底角为30°,腰长为12,则底边上的高AD等于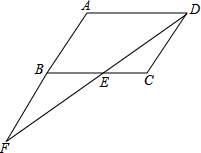 已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.
已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.