题目内容
12.在数学活动课上,九年级(4)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为30°;
(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A、B两点间的距离为5米.请你根据以上数据求出大树CD的高度.
分析 首先分析图形:本题涉及到两个直角三角形△DBC、△ADC,应利用其公共边CD构造等量关系,借助AB=AD-DB=4构造方程关系式,进而可求出答案.
解答 解:设CD=x米,
在Rt△CBD中,tan45°=$\frac{CD}{BD}$,
∴BD=CD=x米
∴AD=AB+BD=(4+x)米
在Rt△ADC中
∵tan∠A=$\frac{CD}{AD}$,即tan30°=$\frac{x}{4+x}$,
解得,x≈5.5,
答:大树CD的高度约为5.5米.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
 如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求:
如图,在平面直角坐标系中,O为坐标原点,点N的坐标为(20,0),点M在第一象限内,且OM=10,sin∠MON=$\frac{3}{5}$.求: 如图所示,船A和船B同时从小岛O出发,船A沿北偏西20°的方向航行,船B沿北偏东70°的方向航行.
如图所示,船A和船B同时从小岛O出发,船A沿北偏西20°的方向航行,船B沿北偏东70°的方向航行.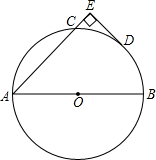 如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,
如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,
