题目内容
(1)化简:
-2
+
;
(2)解方程:2x2-3x-1=0;
(3)已知实数x、y满足y=
-
+3,试求
-
的值.
| 32 |
|
| 0.5 |
(2)解方程:2x2-3x-1=0;
(3)已知实数x、y满足y=
| x-2 |
| 2-x |
| 2 | ||
x+
|
| 2 | ||
x-
|
考点:二次根式的化简求值,二次根式有意义的条件,二次根式的加减法,解一元二次方程-公式法
专题:
分析:(1)首先对二次根式进行化简,然后合并同类二次根式即可求解;
(2)利用求根公式即可求解;
(3)首先根据算术平方根的意义求得x的值,然后求得y的值,把所求的式子进行通分化简,然后把x,y的值代入即可求解.
(2)利用求根公式即可求解;
(3)首先根据算术平方根的意义求得x的值,然后求得y的值,把所求的式子进行通分化简,然后把x,y的值代入即可求解.
解答:解:(1)原式=4
-
+
=4
;
(2)∵a=2,b=-3,c=-1,
则b2-4ac=9+8=17>0,
则x=
,
则x1=
,x2=
;
(3)根据题意得:
,
解得:x=2,
则y=3.
原式=
=
,
当x=2,y=3时,原式=-4
.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)∵a=2,b=-3,c=-1,
则b2-4ac=9+8=17>0,
则x=
3±
| ||
| 4 |
则x1=
3+
| ||
| 4 |
3-
| ||
| 4 |
(3)根据题意得:
|
解得:x=2,
则y=3.
原式=
2(x-
| ||||
| x2-y |
-4
| ||
| x2-y |
当x=2,y=3时,原式=-4
| 3 |
点评:本题考查了二次根式的化简求值以及一元二次方程的解法,二次根式有意义的条件,二次根式的急速那中首先要对二次根式进行化简.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
下列说法正确的是( )
| A、一个数与其倒数之商为-1 | ||
B、a的倒数是
| ||
| C、a的相反数是-a | ||
| D、2a>a(a为有理数) |
下列说法正确的是( )
| A、带根号的数都是无理数 |
| B、不带根号的数都是有理数 |
| C、无理数是无限小数 |
| D、无限小数是无理数 |
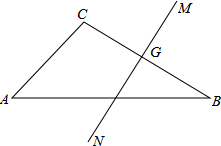 如图,△ABC中,NM是BC边的垂直平分线,垂足为G.
如图,△ABC中,NM是BC边的垂直平分线,垂足为G. 如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E. 在△ABC中,AB=AC,
在△ABC中,AB=AC,