题目内容
 在△ABC中,AB=AC,
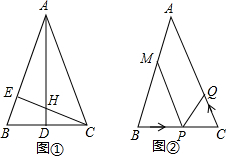
在△ABC中,AB=AC,(1)如图①,若∠BAC=45°,AD和CE是高,它们相交于点H.求证:AH=2BD;
(2)如图②,若AB=AC=10厘米,BC=8厘米,点M为AB的中点,点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.如果在运动过程中存在某一时刻使得△BPM与△CQP全等,那么点Q的运动速度为多少?点P、Q运动的时间t为多少?
考点:全等三角形的判定与性质,等腰三角形的性质
专题:动点型
分析:(1)证得△BCE≌△HAE,证得AH=BC,证得AH=2BD;
(2)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度.
(2)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度.
解答:解:(1)证明:在△ABC中,
∵∠BAC=45°,CE⊥AB,
∴AE=CE,∠EAH=∠ECB,
在△AEH和△CEB中,
,
∴△AEH≌△CEB(ASA),
∴AH=BC,
∵BC=BD+CD,且BD=CD,
∴BC=2BD,
∴AH=2BD.
(2)∵AB=AC,∴∠B=∠C,
∴△BPM与△CQP全等有两种情况:△BPM≌△CPQ 或△BPM≌△CQP
当△BPM≌△CPQ时,BP=PC=4,CQ=BM=5,
∴点P,点Q运动的时间t=
=
秒,
∴vQ=
=
=
厘米/秒.
当△BPM≌△CQP时,BP=CQ,
∴VQ=VP=3厘米/秒.
此时 PC=BM=5,t=
=1秒.
综上所述,点Q的运动速度为
厘米/秒,此时t=
秒或点Q的运动速度为3厘米/秒,此时t=1秒.
∵∠BAC=45°,CE⊥AB,
∴AE=CE,∠EAH=∠ECB,
在△AEH和△CEB中,
|
∴△AEH≌△CEB(ASA),
∴AH=BC,
∵BC=BD+CD,且BD=CD,
∴BC=2BD,
∴AH=2BD.
(2)∵AB=AC,∴∠B=∠C,
∴△BPM与△CQP全等有两种情况:△BPM≌△CPQ 或△BPM≌△CQP
当△BPM≌△CPQ时,BP=PC=4,CQ=BM=5,
∴点P,点Q运动的时间t=
| BP |
| 3 |
| 4 |
| 3 |
∴vQ=
| CQ |
| t |
| 5 | ||
|
| 15 |
| 4 |
当△BPM≌△CQP时,BP=CQ,
∴VQ=VP=3厘米/秒.
此时 PC=BM=5,t=
| BP |
| 3 |
综上所述,点Q的运动速度为
| 15 |
| 4 |
| 4 |
| 3 |
点评:此题考查了全等三角形的判定,等腰三角形的性质.解题时,主要是运用了路程=速度×时间的公式.熟练运用全等三角形的判定和性质,能够分析出追及相遇的问题中的路程关系.

练习册系列答案
相关题目
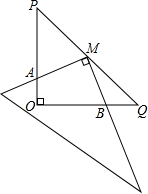 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
 实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).