题目内容
10. 如图,点B、C、E在同一条直线上,△ABC、△DCE都为等边三角形,M为BD的中点,N为AE的中点,求证:△CMN为等边三角形.
如图,点B、C、E在同一条直线上,△ABC、△DCE都为等边三角形,M为BD的中点,N为AE的中点,求证:△CMN为等边三角形.
分析 先根据旋转的性质得出CM=CN,∠BCM=∠ACN,再利用等边三角形的判定证明即可.
解答 证明:△BCD绕点C顺时针旋转60°得到△ACE;△BCM绕点C顺时针旋转60°得到△ACN,
∵△BCM绕点C顺时针旋转60°得到△ACN;
∴由旋转的性质可知,
∴CM=CN,∠BCM=∠ACN,
∵∠BCM+∠ACM=60°,
∴∠ACM+∠ACN=60°,
∴∠MCN=60°,
∴△CMN是等边三角形.
点评 本题考查了等边三角形的判定及性质和旋转的知识,解题的关键是弄清旋转的不变性得到不变量.

练习册系列答案
相关题目
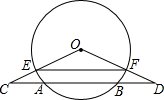 如图,AB是⊙O的弦,C、D是直线AB上的两点,且AC=BD,连接OC、OD,分别交⊙O于E、F两点,试判断EF与CD的位置关系并说明理由.
如图,AB是⊙O的弦,C、D是直线AB上的两点,且AC=BD,连接OC、OD,分别交⊙O于E、F两点,试判断EF与CD的位置关系并说明理由.