题目内容
20.解不等式组:$\left\{\begin{array}{l}{2x+1>-3①}\\{-2x≤x-9②}\end{array}\right.$ 并把解集在数轴上表示出来.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:∵解不等式①,得x>-2,
解不等式②,得x≥3,
∴这个不等式组的解集是x≥3,
把不等式组的解集在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的应用,解此题的关键是能根据找不等式组解集的规律找出不等式组的解集.

练习册系列答案
相关题目
11.若关于x的不等式组$\left\{\begin{array}{l}{5-2x<1}\\{x-a≤0}\end{array}\right.$的整数解只有1个,则a的取值范围是( )
| A. | 2<a<3 | B. | 3≤a<4 | C. | 2<a≤3 | D. | 3<a≤4 |
15.用加减法解方程组$\left\{\begin{array}{l}2x-3y=5,①\\ 3x-2y=7,②\end{array}\right.$下列解法不正确的是( )
| A. | ①×2-②×(-3),消去y | B. | ①×2-②×3,消去y | C. | ①×(-3)+②×2,消去x | D. | ①×3-②×2,消去x |
5. 如图,在数轴上表示的不等式解集为( )
如图,在数轴上表示的不等式解集为( )
 如图,在数轴上表示的不等式解集为( )
如图,在数轴上表示的不等式解集为( )| A. | x>75 | B. | x<75 | C. | x≥75 | D. | x≤75 |
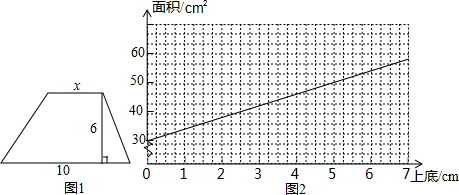
9.如图,梯形的下底是10cm,高是6cm,设梯形的上底为xcm,面积为ycm2,面积y随上底x的变化而变化.
(1)在这个变化过程中,x是自变量,y是因变量.
(2)y与x的关系式为:y=3x+30;
(3)请根据关系式填写表:
(4)小亮用下面的图象来表示面积y与上底x的变化规律,请观察图象回答:梯形的面积y随上底x的增大而增大;若要使面积y大于39cm2,则上底x的范围是3<x<10.

(1)在这个变化过程中,x是自变量,y是因变量.
(2)y与x的关系式为:y=3x+30;
(3)请根据关系式填写表:
| x | 1 | 2 | 2.5 | 5 | 8 |
| y | 33 | 36 | 37.5 | 45 |
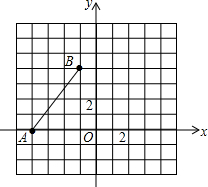 如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.
如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′. 如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) 如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )
如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( ) 如图,点B、C、E在同一条直线上,△ABC、△DCE都为等边三角形,M为BD的中点,N为AE的中点,求证:△CMN为等边三角形.
如图,点B、C、E在同一条直线上,△ABC、△DCE都为等边三角形,M为BD的中点,N为AE的中点,求证:△CMN为等边三角形.