题目内容
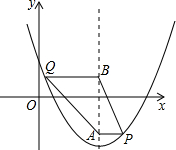 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.(1)求这条抛物线所对应的函数关系式;
(2)求点Q的坐标(用含m的式子表示);
(3)请探究PA+QB=AB是否成立,并说明理由;
(4)抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,若其对称轴把四边形PAQB分成面积比为1:5的两部分,直接写出此时m的值.
考点:二次函数综合题,三角形的面积
专题:综合题
分析:(1)根据经过的点的坐标和对称轴列出关于b、c的方程组,然后求解得到b、c的值,即可得解;
(2)根据点P在抛物线上表示点P的坐标,再求出PA,然后表示出QB,从而求出点Q的横坐标,代入抛物线解析式求出点Q的纵坐标,从而得解;
(3)根据点P、Q的坐标表示出点A、B的坐标,然后分别求出PQ、BQ、AB,即可得解;
(4)根据抛物线的对称性,抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,然后根据四边形PAQB被分成的两个部分列出方程求解即可.
(2)根据点P在抛物线上表示点P的坐标,再求出PA,然后表示出QB,从而求出点Q的横坐标,代入抛物线解析式求出点Q的纵坐标,从而得解;
(3)根据点P、Q的坐标表示出点A、B的坐标,然后分别求出PQ、BQ、AB,即可得解;
(4)根据抛物线的对称性,抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,然后根据四边形PAQB被分成的两个部分列出方程求解即可.
解答:解:(1)∵抛物线y=x2+bx+c经过点(1,-1),且对称轴为在线x=2,
∴
,
解得
.
∴这条抛物线所对应的函数关系式y=x2-4x+2;
(2)∵抛物线上点P的横坐标为m,
∴P(m,m2-4m+2),
∴PA=m-2,
QB=PA+1=m-2+1=m-1,
∴点Q的横坐标为2-(m-1)=3-m,
点Q的纵坐标为(3-m)2-4(3-m)+2=m2-2m-1,
∴点Q的坐标为(3-m,m2-2m-1);
(3)PA+QB=AB成立.
理由如下:∵P(m,m2-4m+2),Q(3-m,m2-2m-1),
∴A(2,m2-4m+2),B(2,m2-2m-1),
∴AB=(m2-2m-1)-(m2-4m+2)=2m-3,
又∵PA=m-2,QB=m-1,
∴PA+QB=m-2+m-1=2m-3,
∴PA+QB=AB;
(4)∵抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,
∴抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,
∵对称轴把四边形PAQB分成面积为1:5的两部分,
∴
×
×
=
×
(2m-3)×(2m-3),
整理得,(2m-3)(m-3)=0,
∵点P位于对称轴右侧,
∴m>2,
∴2m-3≠0,
∴m-3=0,
解得m=3.
∴
|
解得
|
∴这条抛物线所对应的函数关系式y=x2-4x+2;
(2)∵抛物线上点P的横坐标为m,
∴P(m,m2-4m+2),
∴PA=m-2,
QB=PA+1=m-2+1=m-1,
∴点Q的横坐标为2-(m-1)=3-m,
点Q的纵坐标为(3-m)2-4(3-m)+2=m2-2m-1,
∴点Q的坐标为(3-m,m2-2m-1);
(3)PA+QB=AB成立.
理由如下:∵P(m,m2-4m+2),Q(3-m,m2-2m-1),
∴A(2,m2-4m+2),B(2,m2-2m-1),
∴AB=(m2-2m-1)-(m2-4m+2)=2m-3,
又∵PA=m-2,QB=m-1,
∴PA+QB=m-2+m-1=2m-3,
∴PA+QB=AB;
(4)∵抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,
∴抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,
∵对称轴把四边形PAQB分成面积为1:5的两部分,
∴
| 1 |
| 2 |
| m-1 |
| 2 |
| 2m-3 |
| 2 |
| 1 |
| 1+5 |
| 1 |
| 2 |
整理得,(2m-3)(m-3)=0,
∵点P位于对称轴右侧,
∴m>2,
∴2m-3≠0,
∴m-3=0,
解得m=3.
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,抛物线上点的坐标特征,三角形的面积,难点在于(4)根据抛物线的对称性判断出抛物线的对称轴为QB的垂直平分线.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
若二次根式
有意义,则x的取值范围是( )
| ||
| x-1 |
A、x≥-
| ||
| B、x≠1 | ||
| C、x>1 | ||
D、x≥-
|
方程组
的解为
,则a、b分别为( )
|
|
| A、a=8,b=-2 |
| B、a=8,b=2 |
| C、a=12,b=2 |
| D、a=18,b=8 |
 列方程(组)解应用题.
列方程(组)解应用题. 如图,在?ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.