题目内容
 如图,在?ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠BMC=90°,连接AN,DN,AN与BM交于点O.(1)求证:△ABM≌△CDN;
(2)点P在直线BM上,若BM=3,CM=4,求△PND的周长的最小值.
考点:平行四边形的性质,全等三角形的判定与性质,轴对称-最短路线问题
专题:
分析:(1)利用平行四边形的性质首先得出AB=CD,AM=CN,进而得出△ABM≌△CDN;
(2)首先得出平行四边形ABNM为菱形,进而得出当点P位于点M时,NP+DP取到最小值为AD,利用勾股定理求出即可.
(2)首先得出平行四边形ABNM为菱形,进而得出当点P位于点M时,NP+DP取到最小值为AD,利用勾股定理求出即可.
解答:(1)证明:∵在?ABCD中,M,N分别是AD,BC的中点,
∴AB=CD,
在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS);
(2)解:∵在?ABCD中,M,N分别是AD,BC的中点,
∴AM∥BN,AM=NB,
∴四边形ABNM为平行四边形;
在Rt△BCM中,N为BC中点,
∴MN=BN,
∴平行四边形ABNM为菱形.
∴BM垂直平分AN,
∴点N关于BM的对称点为点A.
∴当点P位于点M时,NP+DP取到最小值为AD.
在Rt△BCM中,BM=3,CM=4,
由勾股定理得BC=AD=5,
又由(1)知,BM=DN=3,
∴△PND的周长的最小值:5+3=8.
∴AB=CD,
在△ABM和△CDN中,
|
∴△ABM≌△CDN(SAS);
(2)解:∵在?ABCD中,M,N分别是AD,BC的中点,
∴AM∥BN,AM=NB,
∴四边形ABNM为平行四边形;
在Rt△BCM中,N为BC中点,
∴MN=BN,
∴平行四边形ABNM为菱形.
∴BM垂直平分AN,
∴点N关于BM的对称点为点A.
∴当点P位于点M时,NP+DP取到最小值为AD.
在Rt△BCM中,BM=3,CM=4,
由勾股定理得BC=AD=5,
又由(1)知,BM=DN=3,
∴△PND的周长的最小值:5+3=8.
点评:此题主要考查了全等三角形的判定与性质以及平行四边形和菱形的性质,得出当点P位于点M时,NP+DP取到最小值为AD是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
某校去年有学生1 000名,今年比去年增加4.4%,其中住宿学生增加6%,走读生减少2%.若设该校去年有住宿学生有x名,走读学生有y名,则根据题意可得方程组( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
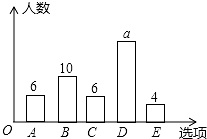 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )
为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )| A、全面调查;26 |
| B、全面调查;24 |
| C、抽样调查;26 |
| D、抽样调查;24 |
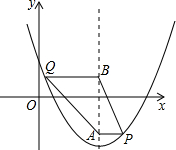 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.