题目内容
已知如图,AB∥CD,直线l分别截AB、CD于E、C两点,M是线段EC上一动点(不与E、C重合),过M点作MN⊥CD于点N,连结EN.

(1)如图1,当∠ECD=30°时,直接写出∠MEN+∠MNE的度数;
(2)如图2,当∠ECD=α°时,猜想∠MEN+∠MNE的度数与α的关系,并证明你的结论.

(1)如图1,当∠ECD=30°时,直接写出∠MEN+∠MNE的度数;
(2)如图2,当∠ECD=α°时,猜想∠MEN+∠MNE的度数与α的关系,并证明你的结论.
考点:平行线的性质,三角形的外角性质,直角三角形的性质
专题:
分析:(1)在直角△MNE中,利用直角三角形的两锐角互余,即可求得∠CMN的度数,然后利用三角形的外角的性质求解;
(2)方法与(1)相同.
(2)方法与(1)相同.
解答:解:(1)∵MN⊥CD,
∴直角△MNE中,∠CMN=90°-∠ECD=90°-30°=60°,
∴∠CMN=∠MEN+∠MNE=60°;
(2)同(1)可得:∠CMN=∠MEN+∠MNE=90°-α°.
∵MN⊥CD,
∴直角△MNE中,∠CMN=90°-∠ECD=90°-α°,
∴∠CMN=∠MEN+∠MNE=90°-α°.
∴直角△MNE中,∠CMN=90°-∠ECD=90°-30°=60°,
∴∠CMN=∠MEN+∠MNE=60°;
(2)同(1)可得:∠CMN=∠MEN+∠MNE=90°-α°.
∵MN⊥CD,
∴直角△MNE中,∠CMN=90°-∠ECD=90°-α°,
∴∠CMN=∠MEN+∠MNE=90°-α°.
点评:本题考查了直角三角形的性质,以及三角形的外角的性质:三角形的外角等于两个不相邻的两个内角的和.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a6÷a2=a3 |
| B、a3•a3•a3=3a3 |
| C、(a3)4=a12 |
| D、(a+2b)2=a2+4b2 |
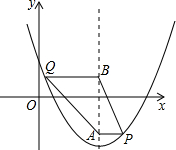 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.