题目内容
 如图,在第一象限内,点P(2,3)、M(a,2)是双曲线y=
如图,在第一象限内,点P(2,3)、M(a,2)是双曲线y=| k |
| x |
| 5 |
| 3 |
| 5 |
| 3 |
分析:由于点P(2,3)在双曲线y=
(k≠0)上,首先利用待定系数法求出k的值,得到反比例函数的解析式,把y=2代入,求出a的值,得到点M的坐标,然后利用待定系数法求出直线OM的解析式,把x=2代入,求出对应的y值即为点C的纵坐标,最后根据直角梯形的面积公式求出四边形ABMC的面积.
| k |
| x |
解答: 解:如图,∵PA⊥x,MB⊥x,
解:如图,∵PA⊥x,MB⊥x,
∴AC∥MB,
∵MC与AB不平行,
∴四边形ABMC是直角梯形.
∵点P(2,3)在双曲线y=
(k≠0)上,
∴k=2×3=6,
∴y=
,
当y=2时,x=3,即M(3,2).
∴直线OM的解析式为y=
x,
当x=2时,y=
,即C(2,
).
∴AB=1,AC=
,BM=2,
∴S梯形ABMC=
(AC+BM)•AB=
×(
+2)×1=
,即四边形ABMC的面积为
.
故答案是:
.
 解:如图,∵PA⊥x,MB⊥x,
解:如图,∵PA⊥x,MB⊥x,∴AC∥MB,
∵MC与AB不平行,
∴四边形ABMC是直角梯形.
∵点P(2,3)在双曲线y=
| k |
| x |
∴k=2×3=6,
∴y=
| 6 |
| x |
当y=2时,x=3,即M(3,2).
∴直线OM的解析式为y=
| 2 |
| 3 |
当x=2时,y=
| 4 |
| 3 |
| 4 |
| 3 |
∴AB=1,AC=
| 4 |
| 3 |
∴S梯形ABMC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
故答案是:
| 5 |
| 3 |
点评:本题考查用待定系数法求函数的解析式及求图象交点的坐标及三角形的面积,属于一道中等综合题.

练习册系列答案
相关题目
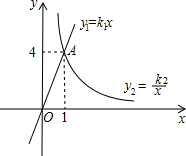 如图,在第一象限内,正比例函数y1=k1x与反比例函数y2=
如图,在第一象限内,正比例函数y1=k1x与反比例函数y2=| k2 |
| x |
| A、0<x<4 | B、0<x<1 |
| C、x>0 | D、x>1 |
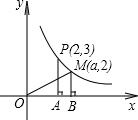 如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=
如图,在第一象限内,点P(2,3),M(a,2)是双曲线y= 如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H,得到△AOH.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形△POQ与△AOH全等,则符合条件的△AOH的面积是
如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H,得到△AOH.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形△POQ与△AOH全等,则符合条件的△AOH的面积是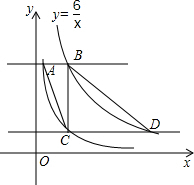 如图,在第一象限内,双曲线
如图,在第一象限内,双曲线