题目内容
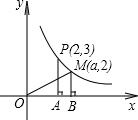 如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=
如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=| k |
| x |
分析:先根据反比例函数图象上点的坐标特征求出k=6,a=3,再利用待定系数法求出直线OM的解析式为y=
x,然后确定C点坐标,再根据三角形面积公式求解.
| 2 |
| 3 |
解答:解:把P(2,3),M(a,2)代入y=
得k=2×3=2a,解得k=6,a=3,
设直线OM的解析式为y=mx,
把M(3,2)代入得3m=2,解得m=
,
所以直线OM的解析式为y=
x,当x=2时,y=
×2=
,
所以C点坐标为(2,
),
所以△OAC的面积=
×2×
=
.
故选B.
| k |
| x |
设直线OM的解析式为y=mx,
把M(3,2)代入得3m=2,解得m=
| 2 |
| 3 |
所以直线OM的解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
所以C点坐标为(2,
| 4 |
| 3 |
所以△OAC的面积=
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
故选B.
点评:本题考查了反比例函数y=
(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
| k |
| x |

练习册系列答案
相关题目
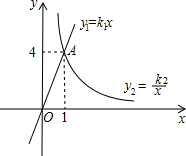 如图,在第一象限内,正比例函数y1=k1x与反比例函数y2=
如图,在第一象限内,正比例函数y1=k1x与反比例函数y2=| k2 |
| x |
| A、0<x<4 | B、0<x<1 |
| C、x>0 | D、x>1 |
 如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H,得到△AOH.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形△POQ与△AOH全等,则符合条件的△AOH的面积是
如图,在第一象限内作射线OC,与x轴的夹角为30°,在射线OC上取一点A,过点A作AH⊥x轴于点H,得到△AOH.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形△POQ与△AOH全等,则符合条件的△AOH的面积是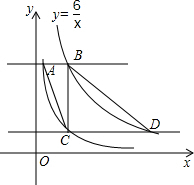 如图,在第一象限内,双曲线
如图,在第一象限内,双曲线