题目内容
1.用一根铁丝围成一个长方形,使长方形的一边长为6厘米且长方形的面积不小于12平方厘米,则该铁丝至少长16厘米.分析 设该长方形的宽为x,根据长方形的面积公式得到不等式6x≥12,由此求得长方形的宽的最小值,然后由长方形的周长公式求得该铁丝的长度即可.
解答 解:设该长方形的宽为x,
依题意得:6x≥12,
解得x≥2,
则x的最小值是2,即该长方形的宽最小为2厘米,
所以该铁丝的长为:2×(6+2)=16(厘米).
故答案是:16.
点评 本题考查了一元一次不等式的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系.

练习册系列答案
相关题目
11. 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D,过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE,对于下列结论:①AD=AE;②△CBA∽△CDE;③弧BD=$\frac{2}{3}$弧AD;④AE为⊙O的切线,结论一定正确的是( )| A. | ②③ | B. | ②④ | C. | ①② | D. | ①③ |
16.已知P(x,y)在第二象限,且x2=4,|y|=7,则点P的坐标是( )
| A. | (2,-7) | B. | (-4,7) | C. | (4,-7) | D. | (-2,7) |
13.在下列命题中,真命题的是( )
| A. | 同位角相等 | |
| B. | $\sqrt{4}$=±2 | |
| C. | 三角形的外角等于它相邻的两个内角之和 | |
| D. | 无理数是无限小数 |
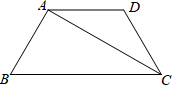 如图,AD∥BC,AC是∠BCD的平分线,∠BCD=60°,∠BAD=120°.
如图,AD∥BC,AC是∠BCD的平分线,∠BCD=60°,∠BAD=120°.