题目内容
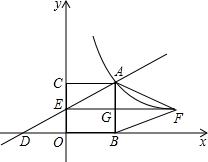 如图,过反比例函数y=
如图,过反比例函数y=| 4 | x |
(1)求点A的坐标和一次函数解析式;
(2)求四边形ADBF的面积;
(3)猜想线段DE和线段BF有怎样的关系,并加以证明.
分析:(1)根据反比函数比例系数k的几何意义,求出正方形ABOC的面积,利用OB=OA,求出A的坐标;将A的坐标代入解析式即可求出一次函数中k的值,从而得到一次函数解析式;
(2)计算出E点坐标、F点坐标,求出DB、AB、GF的长,计算出S△ADB+S△ABF的值即为四边形ADBF的面积.
(3)根据E、F及D、B的坐标,求出EF和DB的长,再根据EF∥DB,判断出四边形DBFE为平行四边形,从而得到线段DE和线段BF的关系.
(2)计算出E点坐标、F点坐标,求出DB、AB、GF的长,计算出S△ADB+S△ABF的值即为四边形ADBF的面积.
(3)根据E、F及D、B的坐标,求出EF和DB的长,再根据EF∥DB,判断出四边形DBFE为平行四边形,从而得到线段DE和线段BF的关系.
解答:解:(1)∵点A在反比例函数y=
图象上,
反比例函数比例系数为4,
则正方形ABOC的面积为4,
即OB×AB=4,
AB=OB=2,
A点坐标为(2,2).
将A(2,2)代入y=kx+1得,2k+1=2,k=
,
函数解析式为y=
x+1.
(2)设E点坐标为(0,e),代入y=
x+1得,e=1.
由于EF∥x轴,
可得F点纵坐标为1,
将y=1代入y=
得,x=4,F点坐标为(4,1).
设D点坐标为(d,0),代入y=
x+1得,0=
d+1,
d=-2,D点坐标为(-2,0).
S四边形ADBF=S△ADB+S△ABF=
×4×2+
×2×2=4+2=6.
(3)∵EF=DB=4,EF∥DB,
∴四边形DBFE为平行四边形,
则DE与BF平行且相等.
| 4 |
| x |

反比例函数比例系数为4,
则正方形ABOC的面积为4,
即OB×AB=4,
AB=OB=2,
A点坐标为(2,2).
将A(2,2)代入y=kx+1得,2k+1=2,k=
| 1 |
| 2 |
函数解析式为y=
| 1 |
| 2 |
(2)设E点坐标为(0,e),代入y=
| 1 |
| 2 |
由于EF∥x轴,
可得F点纵坐标为1,
将y=1代入y=
| 4 |
| x |
设D点坐标为(d,0),代入y=
| 1 |
| 2 |
| 1 |
| 2 |
d=-2,D点坐标为(-2,0).
S四边形ADBF=S△ADB+S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵EF=DB=4,EF∥DB,
∴四边形DBFE为平行四边形,
则DE与BF平行且相等.
点评:本题考查了反比例函数综合题,涉及待定系数法求函数解析式、反比例函数k的几何意义、平行四边形的判定和性质、坐标与函数的关系等,要结合图形进行探究方可顺利解答.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
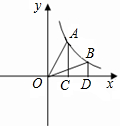 如图,过反比例函数y=
如图,过反比例函数y=| 9 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
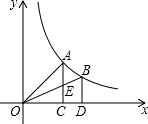 如图,过反比例函数y=
如图,过反比例函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、Sl<S2 |
| D、大小关系不能确定 |
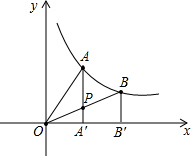 如图,过反比例函数y=
如图,过反比例函数y=| 2 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
 如图,过反比例函数
如图,过反比例函数 如图,过反比例函数y=
如图,过反比例函数y=