题目内容
7. 如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为8.
如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为8.
分析 根据题意可以求得∠BAE的度数,由正六边形ABCDEF内接于半径为4的圆,可以求得B、E两点间的距离.
解答  解:连接BE、AE,如右图所示,
解:连接BE、AE,如右图所示,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠AFE=120°,FA=FE,
∴∠FAE=∠FEA=30°,
∴∠BAE=90°,
∴BE是正六边形ABCDEF的外接圆的直径,
∵正六边形ABCDEF内接于半径为4的圆,
∴BE=8,
即则B、E两点间的距离为8,
故答案为:8.
点评 本题考查正多边形和圆,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (-2a3)2=-4a6 | B. | $\sqrt{9}$=±3 | C. | m2•m3=m6 | D. | x3+2x3=3x3 |
19.月球的直径约为3476000米,将3476000用科学记数法表示应为( )
| A. | 0.3476×102 | B. | 34.76×104 | C. | 3.476×106 | D. | 3.476×108 |
17.关于x的一元二次方程x2+4x+k=0有两个相等的实根,则k的值为( )
| A. | k=-4 | B. | k=4 | C. | k≥-4 | D. | k≥4 |
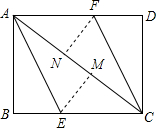 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.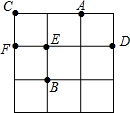 如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$.
如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$. 如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )
如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( ) 如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.