题目内容
3.现要在墙上钉一根水平方向的木条,至少需要2个钉子,其道理用数学知识解释为两点确定一条直线;把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是两点之间线段最短.分析 分别利用线段的性质以及直线的性质分别分析得出答案.
解答 解:现要在墙上钉一根水平方向的木条,至少需要2个钉子,其道理用数学知识解释为:两点确定一条直线;
把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释应是:两点之间线段最短.
故答案为:两点确定一条直线;两点之间线段最短.
点评 此题主要考查了线段的性质以及直线的性质,记住常见的几何中的定理及其实际中的应用类型是解决此类问题的方法.

练习册系列答案
相关题目
13.在-6,7,8,-$\frac{1}{9}$,12,0,-0.33,$\frac{2}{5}$各数中,负分数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14. 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 2:5 | D. | 4:9 |
13.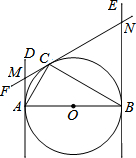 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
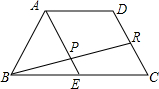 如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.
如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP=$\frac{1}{3}$.