题目内容
19.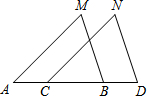 如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.
如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.
分析 根据平行线的性质求出∠MAB=∠NCD,根据ASA推出△MAB≌△NCD,根据全等三角形的性质推出AB=CD即可.
解答 证明:∵MA∥NC,
∴∠MAB=∠NCD,
在△MAB和△NCD中
$\left\{\begin{array}{l}{∠MAB=∠NCD}\\{AM=NC}\\{∠M=∠N}\end{array}\right.$
∴△MAB≌△NCD(ASA),
∴AB=CD,
∴AB-BC=CD-BC,
∴AC=BD.
点评 本题考查了全等三角形的性质和判定,平行线的性质的应用,能推出△MAB≌△NCD是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
14.Rt△ABC中,∠C=90°,AC=3,BC=4,则中线CD的长是( )
| A. | 2 | B. | 2.5 | C. | 5 | D. | 1.5 |
8.已知5a2mb和3a4b3-n是同类项,则2m-n的值是( )
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
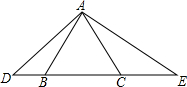 如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.
如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.