题目内容
 如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.
如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.考点:三角形的外角性质,三角形内角和定理
专题:
分析:根据角平分线的定义可得∠ACD=
∠BCA=
∠A,然后根据直角三角形两锐角互余列出方程求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵CD平分∠ACB,
∴∠ACD=
∠BCA=
∠A,
∵CE⊥AB,
∴∠A+∠ACD+∠DCE=90°,
∴∠A+
∠A+54°=90°,
解得∠A=24°.
∴∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∵CE⊥AB,
∴∠A+∠ACD+∠DCE=90°,
∴∠A+
| 1 |
| 2 |
解得∠A=24°.
点评:本题考查了三角形的内角和定理,角平分线的定义,利用∠A表示出∠ACD是解题的关键.

练习册系列答案
相关题目
 在四边形ABCD中,已知AB∥CD,∠B=60°,
在四边形ABCD中,已知AB∥CD,∠B=60°,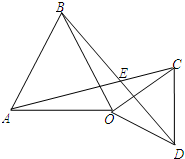 已知,△OAB和△OCD都是等边三角形,若△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转到如图位置,连结AC,BD,AC与BD相交于点E.
已知,△OAB和△OCD都是等边三角形,若△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转到如图位置,连结AC,BD,AC与BD相交于点E. 如图,△ABC中,AB=AC,点D、点E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数.
如图,△ABC中,AB=AC,点D、点E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数.