题目内容
 如图,△ABC中,AB=AC,点D、点E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数.
如图,△ABC中,AB=AC,点D、点E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数.考点:等腰三角形的性质
专题:
分析:根据等边对等角可得∠ADE=∠A,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠A+∠ADE=2∠A,根据等边对等角可得∠BED=∠EBD,再利用三角形的一个外角等于与它不相邻的两个内角的和可得∠BDC=∠A+∠EBD=3∠A,再次利用等边对等角可得∠BDC=∠C,∠ABC=∠C,然后利用三角形的内角和等于180°列出方程求解即可.
解答:解:∵DE=EA,
∴∠ADE=∠A,
∴∠BED=∠A+∠ADE=2∠A,
∵BD=DE,
∴∠BED=∠EBD=2∠A,
∴∠BDC=∠A+∠EBD=3∠A,
∵BC=BD,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C=3∠A,
在△ABC中,∠A+∠ABC+∠C=∠A+3∠A+3∠A=180°,
解得∠A=
.
∴∠ADE=∠A,
∴∠BED=∠A+∠ADE=2∠A,
∵BD=DE,
∴∠BED=∠EBD=2∠A,
∴∠BDC=∠A+∠EBD=3∠A,
∵BC=BD,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C=3∠A,
在△ABC中,∠A+∠ABC+∠C=∠A+3∠A+3∠A=180°,
解得∠A=
| 180° |
| 7 |
点评:本题考查了三角形的内角和定理,等边对等角和三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
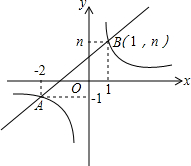 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.
如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.