题目内容
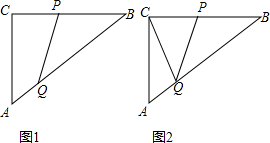
已知:如图①,在Rt△ACB中,∠C=90°,AC=6cm,BC=8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s;点 Q由A出发沿AB方向向点B匀速运动,速度为1cm/s;连接PQ.若设运动的时间为t (s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ的垂直平分线经过点B?
(2)如图②,连接CQ.设△PQC的面积为y(cm2),求y与t之间的函数关系式;
(3)如图②,是否存在某一时刻t,使线段CQ恰好把四边形ACPQ的面积分成1:2的两部分?若存在,求出此时t的值;若不存在,说明理由.
(1)当t为何值时,PQ的垂直平分线经过点B?
(2)如图②,连接CQ.设△PQC的面积为y(cm2),求y与t之间的函数关系式;
(3)如图②,是否存在某一时刻t,使线段CQ恰好把四边形ACPQ的面积分成1:2的两部分?若存在,求出此时t的值;若不存在,说明理由.

考点:相似形综合题
专题:
分析:(1)根据勾股定理,可得AB的长,根据线段垂直平分线上的点到线段两端点的距离相等,可得方程,根据解方程,可得答案;
(2)根据相似三角形的判定与性质,可得QD的长,根据三角形的面积公式,可得函数解析式;
(3)根据三角形面积的和差,可得四边形的面积,根据线段CQ恰好把四边形ACPQ的面积分成1:2的两部分,可得方程,根据解方程,可得答案.
(2)根据相似三角形的判定与性质,可得QD的长,根据三角形的面积公式,可得函数解析式;
(3)根据三角形面积的和差,可得四边形的面积,根据线段CQ恰好把四边形ACPQ的面积分成1:2的两部分,可得方程,根据解方程,可得答案.
解答:解:(1)由勾股定理得AB=
=10,
由题意得PB=2t,QB=10-t,
由PQ的垂直平分线经过点B,得
2t=10-t,
t=
;
(2)作QD⊥BC与D点,AC⊥BC, ,
,
QD∥AC,
△BDQ∽△BCQ,
=
,AC=6,AB=10,BQ=10-t,
DQ=
,CP=8-2t,
y=
CP•DQ=
×
×(8-2t),
即y=-
t2-
t+24;
(3)存在,
S△BCQ=
BC•DQ=
×8×
=24-
t,
S△ABC=
×AC×BC=24,
S△ACQ=S△ABC-S△CQB=24-(24-
t)=
t,
①当S△ACQ:SCPQ=1:2时,(
t):(-
t2-
t+24)=1:2,
t2+22t-40=0
解得t1=-11+
,t2=-11-
(不符合题意舍去),
②当S△ACQ:SCPQ=2:1时,(
t):(-
t2-
t+24)=2:1,
t2+16t-40=0
解得t1=-8+2
,t2=-8-2
(不符合题意,舍去),
综上所述:t=-11+
,t=-8+2
时线段CQ恰好把四边形ACPQ的面积分成1:2的两部分.
| AC2+BC2 |
由题意得PB=2t,QB=10-t,
由PQ的垂直平分线经过点B,得
2t=10-t,
t=
| 10 |
| 3 |
(2)作QD⊥BC与D点,AC⊥BC,
 ,
,QD∥AC,
△BDQ∽△BCQ,
| BQ |
| AB |
| DQ |
| AC |
DQ=
| 30-3t |
| 5 |
y=
| 1 |
| 2 |
| 1 |
| 2 |
| 30-3t |
| 5 |
即y=-
| 3 |
| 5 |
| 42 |
| 5 |
(3)存在,
S△BCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 30-3t |
| 5 |
| 12 |
| 5 |
S△ABC=
| 1 |
| 2 |
S△ACQ=S△ABC-S△CQB=24-(24-
| 12 |
| 5 |
| 12 |
| 5 |
①当S△ACQ:SCPQ=1:2时,(
| 12 |
| 5 |
| 3 |
| 5 |
| 42 |
| 5 |
t2+22t-40=0
解得t1=-11+
| 161 |
| 161 |
②当S△ACQ:SCPQ=2:1时,(
| 12 |
| 5 |
| 3 |
| 5 |
| 42 |
| 5 |
t2+16t-40=0
解得t1=-8+2
| 26 |
| 26 |
综上所述:t=-11+
| 161 |
| 26 |
点评:本题考查了相似形综合题,利用了线段垂直平分线的性质,相似三角形的判定与性质,一元二次方程的解法,构造相似三角形是解题关键.

练习册系列答案
相关题目
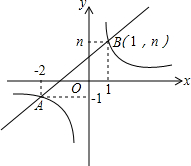 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.
如图,△ABC中,∠BAC=∠BCA,CD平分∠ACB,CE⊥AB交AB的延长线于点E,若∠DCE=54°,求∠A的度数.