题目内容
如图，小方格的边长为1，点A，B，C均在格点上，求△ABC的周长和面积．考点：勾股定理
专题：
分析：根据勾股定理求得△ABC的三条边长后，再来求该三角形的周长；直接根据三角形的面积公式求解．
解答：解：由勾股定理可知，
BC=
=
，
AC=
=
，
则△ABC的周长为
+
+4，
面积为4×2÷2=4．
BC=
| 12+22 |
| 5 |
AC=
| 22+32 |
| 13 |
则△ABC的周长为
| 13 |
| 5 |
面积为4×2÷2=4．
点评：本题考查了直角三角形中勾股定理的运用，本题中运用勾股定理准确计算AB、AC和BC的长是解题的关键．
练习册系列答案
相关题目
下列判断正确的是（ ）
| A、两个直角三角形必全等 |
| B、两个等腰三角形必全等 |
| C、顶角相等的两个等腰三角形全等 |
| D、有一边相等的两个等边三角形全等 |
在四边形ABCD中，AD∥BC，且AD=8cm，BC=6cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C出发向B运动，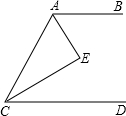
如图，AE、CE平分∠BAC、∠ACD，且∠E=90°，那么AB∥CD，这个结论对吗？为什么？