题目内容
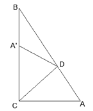
【题目】如图,![]() ,
,![]() 是
是![]() 、
、![]() 的角平分线交点,
的角平分线交点,![]() 是
是![]() 、
、![]() 外角平分线交点,则
外角平分线交点,则![]() ______
______![]() ,
,![]() _____
_____![]() ,联结
,联结![]() ,则
,则![]() ______
______![]() ,点
,点![]() ____(选填“在”、“不在”或“不一定在”)直线
____(选填“在”、“不在”或“不一定在”)直线![]() 上.
上.

【答案】116 64 26 在
【解析】
∠ABC+∠ACB=180°-∠A,∠OBC+∠OCB= ![]() (∠ABC+∠ACB), ∠BOC=180°-(∠OBC+∠OCB),据此可求∠BOC的度数;
(∠ABC+∠ACB), ∠BOC=180°-(∠OBC+∠OCB),据此可求∠BOC的度数;
∠BCP= ![]() ∠BCE=
∠BCE= ![]() (∠A+∠ABC),∠PBC=
(∠A+∠ABC),∠PBC= ![]() ∠CBF=
∠CBF= ![]() (∠A+∠ACB),由三角形内角和定理得:∠BPC=180°-∠BCP-∠PBC,据此可求∠BPC的度数;
(∠A+∠ACB),由三角形内角和定理得:∠BPC=180°-∠BCP-∠PBC,据此可求∠BPC的度数;
作PG⊥AB于G,PH⊥AC于H,PK⊥BC于K,利用角平分线的性质定理可证明PG=PH,于是可证得AP平分∠BAC,据此可求∠PAB的度数;
同理可证OA平分∠BAC,故点![]() 在直线
在直线![]() 上.
上.
解:∵O点是∠ABC和∠ACB的角平分线的交点,
∴∠OBC+∠OCB= ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
= ![]() (180°-∠A)
(180°-∠A)
=90°- ![]() ∠A,
∠A,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-90°+ ![]() ∠A
∠A
=90°+ ![]() ∠A
∠A
=90°+26°
=116°;
如图,
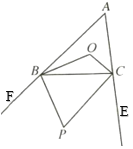
∵BP、CP为△ABC两外角的平分线,
∴∠BCP= ![]() ∠BCE=
∠BCE= ![]() (∠A+∠ABC),
(∠A+∠ABC),
∠PBC= ![]() ∠CBF=
∠CBF= ![]() (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得:
∠BPC=180°-∠BCP-∠PBC
=180°- ![]() [∠A+(∠A+∠ABC+∠ACB)]
[∠A+(∠A+∠ABC+∠ACB)]
=180°- img src="https://thumb.zyjl.cn/questionBank/Upload/2020/11/27/11/a71e7e8e/SYS202011271140551445817129_DA/SYS202011271140551445817129_DA.001.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />(∠A+180°)
=90°- ![]() ∠A
∠A
=90°-26°
=64°.
如图,作PG⊥AB于G,PH⊥AC于H,PK⊥BC于K,连接AP,
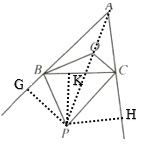
∵BP、CP为△ABC两外角的平分线,PG⊥AB,PH⊥AC,PK⊥BC,
∴PG=PK,PK=PH,
∴PG=PH,
∴AP平分∠BAC,
∴![]() 26°
26°
同理可证OA平分∠BAC,
点![]() 在直线
在直线![]() 上.
上.
故答案是:(1) 116 ;(2) 64;(3) 26;(4) 在.

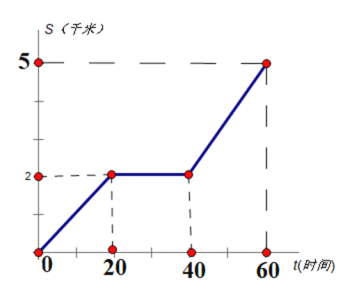
【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)有下面的关系:
(千克)有下面的关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么弹簧的总长![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式.