Question

【题目】甲、乙两人同时从A地前往相距5千米的B地，甲骑自行车，途中修车耽误了20分钟，甲行驶的路程s（千米）关于时间t（分钟）的函数图像如图所示；乙慢跑所行的路程s（千米）关于时间t（分钟）的函数解析式为

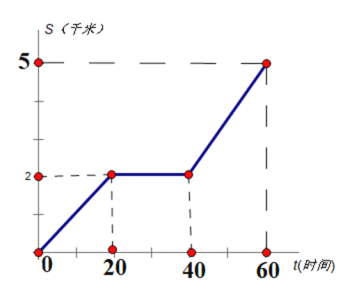
（1）在图中画出乙慢跑所行的路程关于时间的函数图像：

（2）甲修车后行驶的速度是每分钟_______米;

（3）甲、乙两人在出发后，中途_________分钟时相遇

Answer 1

【答案】（1）见解析；（2）150；（3）24.

【解析】

（1）根据两点法画函数图像即可；

（2）根据图像即可求出甲修车后行驶的速度；

（3）由图像可知：相遇时，甲正在修车，此时甲行驶了2千米，然后将s=2代入中，即可求出中途相遇的时间.

解：（1）如图所示：列表如下

t	0	60
s	0	5

乙慢跑所行的路程关于时间的函数图像如下图所示：

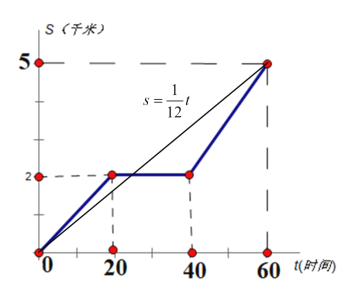
（2）由图像可知：甲修车后行驶的速度是（5－2）÷（60－40）=0.15千米/分=150米/分.

故答案为：150.

（3）由图像可知：相遇时，甲正在修车，此时甲行驶了2千米

将s=2代入中，解得：

故答案为24.