Question

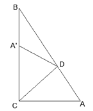
【题目】如图Rt△ABC中∠ACB=90°,将其折叠使点A落在边BC的点A′处,折痕为CD,若∠A′DB=20°,则∠B=（ ）

A.45°B.35°C.30°D.40°

Answer 1

【答案】B

【解析】

首先根据折叠的性质得出∠ACD=∠A′CD，∠ADC=∠A′DC，然后由∠ACB=90°, ∠A′DB=20°,得出∠ACD=∠A′CD=45°，∠ADC=∠A′DC=80°，进而得出∠BDC，最后根据三角形内角和定理，即可得出∠B.

由折叠的性质，得

∠ACD=∠A′CD，∠ADC=∠A′DC

又∵∠ACB=90°, ∠A′DB=20°,

∴∠ACD=∠A′CD=45°，∠ADC=∠A′DC=80°

∴∠BDC=∠A′DB+∠A′DC=100°

∴∠B=180°-∠BDC-∠A′CD=180°-100°-45°=35°

故答案为B.