题目内容
列方程解应用题.
甲、乙两城相距1000千米,一列快车从甲城出发开往乙城,另一列动车从乙城出发开往甲城,两车同时出发,2小时后两车相遇.若动车每小时行驶的路程是快车每小时行驶的路程的1.5倍,求快车平均每小时行驶多少千米?
甲、乙两城相距1000千米,一列快车从甲城出发开往乙城,另一列动车从乙城出发开往甲城,两车同时出发,2小时后两车相遇.若动车每小时行驶的路程是快车每小时行驶的路程的1.5倍,求快车平均每小时行驶多少千米?
考点:一元一次方程的应用
专题:
分析:设快车平均每小时行驶x千米,则动车平均每小时行驶1.5x千米,根据“两车同时出发,2小时后两车相遇”列出方程,解方程即可.
解答:解:设快车平均每小时行驶x千米,则动车平均每小时行驶1.5x千米,根据题意得
2(x+1.5x)=1000,
解得x=200.
答:快车平均每小时行驶200千米.
2(x+1.5x)=1000,
解得x=200.
答:快车平均每小时行驶200千米.
点评:此题考查了一元一次方程的应用,培养了学生应用数学解决生活中实际问题的能力,根据已知表示出两车行驶的总路程是解题关键.

练习册系列答案
相关题目
下列单项式中,次数为5的是( )
| A、3a5b2 |
| B、-2a4b |
| C、-22a2b |
| D、4πa3b |
袋子里有同样大小的4个小球,其中3个红球,1个白球,从袋中任意同时摸出两个小球,则这两个小球颜色相同的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB∥CD,∠A=35°,∠C=80°,那么∠E等于( )
如图,AB∥CD,∠A=35°,∠C=80°,那么∠E等于( )| A、35° | B、45° |
| C、55° | D、75° |
若n是正整数,则[1-(-1)n]n的值一定是( )
| A、零 | B、偶数 |
| C、奇数 | D、是零或奇数 |
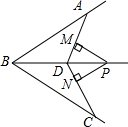 如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.
如图所示,BD是∠ABC的平分线,点P在射线BD上,PM⊥AD于M,PN⊥CD于N,PM=PN,求证:AB=CB.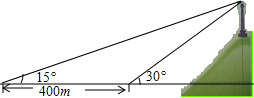 如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗? 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.求证:
如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.求证: