题目内容
 如图,∠A=60°,BD平分∠ABC,CD是△ABC的外角∠ACE的平分线,BD交CD于点D,求∠D的度数.
如图,∠A=60°,BD平分∠ABC,CD是△ABC的外角∠ACE的平分线,BD交CD于点D,求∠D的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACE和∠DCE,再根据角平分线的定义表示出∠DBC和∠DCE,然后整理得到∠D=
∠A,代入数据进行计算即可得解.
| 1 |
| 2 |
解答:解:由三角形外角性质,∠ACE=∠A+∠ABC,∠DCE=∠DBC+∠D,
∵BD、CD分别平分∠ABC和∠ACE,
∴∠DBC=
∠ABC,∠DCE=
∠ACE,
∴
∠A+
∠ABC=
∠ABC+∠D,
∴∠D=
∠A,
∵∠A=60°,
∴∠D=30°.
∵BD、CD分别平分∠ABC和∠ACE,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠D=
| 1 |
| 2 |
∵∠A=60°,
∴∠D=30°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
已知点A(a,b)在第三象限,则点B(-a+1,3b-1)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
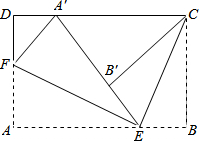 如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( )
如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( ) 将等腰Rt△ABC和等腰Rt△DEF如图摆放,P、M、N是AD、BE、CF的中点,求证:PM=PM且PM⊥PN.
将等腰Rt△ABC和等腰Rt△DEF如图摆放,P、M、N是AD、BE、CF的中点,求证:PM=PM且PM⊥PN. 如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,且∠CAD:∠CAB=1:3,求∠B的度数.
如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,且∠CAD:∠CAB=1:3,求∠B的度数.