题目内容
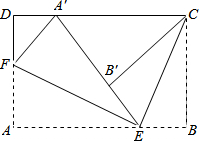 如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( )
如图所示,将矩形纸片ABCD按如图方式折叠,EF、EC为折痕,折叠后点A落在边CD的A处,点B落在边A′E的B′处.若A′D=4,BC=8,则AE的长是( )| A、10 | B、11 | C、12 | D、13 |
考点:翻折变换(折叠问题)
专题:
分析:根据矩形的对边相等可得AD=BC,根据翻折的性质可得AF=A′F,B′C=BC,设AF=x,表示出DF,然后在Rt△A′DF中,利用勾股定理列出方程求解得到AF,再求出DF,然后求出△A′DF和△CB′A′相似,再根据相似三角形对应边成比例列式求出A′B′,利用勾股定理列式求出A′C,然后求出CD,从而得到AB,设AE=y,表示出BE,再根据△AEF和△BCE相似,利用相似三角形对应边成比例列式求解即可.
解答:解:∵矩形ABCD的边BC=8,
∴AD=BC=8,
由翻折的性质得,AF=A′F,B′C=BC,
设AF=x,则DF=8-x,
在Rt△A′DF中,由勾股定理得,A′D2+DF2=A′F2,
即42+(8-x)2=x2,
解得x=5,
∴DF=8-x=8-5=3,
由翻折得,∠EA′F=∠A=90°,∠CB′E=∠B=90°,CB′=BC=8,
∴∠DA′F+∠CA′B′=90°,∠A′B′C=90°,
∵∠DA′F+∠A′FD=90°,
∴∠A′FD=∠CA′B′,
又∵∠D=∠A′B′C=90°,
∴△A′DF∽△CB′A′,
∴
=
,
即
=
,
解得A′B′=6,
由勾股定理得,A′C=
=
=10,
∴CD=A′D+A′C=4+10=14,
∴AB=CD=14,
设AE=y,则BE=14-y,
由翻折的性质得,∠AEF=∠A′EF,∠BEC=∠B′EC,
∴∠AEF+∠BEC=90°,
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEC,
又∵∠A=∠B=90°,
∴△AEF∽△BCE,
∴
=
,
即
=
,
整理得,y2-14y+40=0,
解得y1=4,y2=10,
由图可知,AE大于AB的一半,
所以AE=10.
故选A.
∴AD=BC=8,
由翻折的性质得,AF=A′F,B′C=BC,
设AF=x,则DF=8-x,
在Rt△A′DF中,由勾股定理得,A′D2+DF2=A′F2,
即42+(8-x)2=x2,
解得x=5,
∴DF=8-x=8-5=3,
由翻折得,∠EA′F=∠A=90°,∠CB′E=∠B=90°,CB′=BC=8,
∴∠DA′F+∠CA′B′=90°,∠A′B′C=90°,
∵∠DA′F+∠A′FD=90°,
∴∠A′FD=∠CA′B′,
又∵∠D=∠A′B′C=90°,
∴△A′DF∽△CB′A′,
∴
| DF |
| A′B′ |
| A′D |
| CB′ |
即
| 3 |
| A′B′ |
| 4 |
| 8 |
解得A′B′=6,
由勾股定理得,A′C=
| A′B′2+CB′2 |
| 62+82 |
∴CD=A′D+A′C=4+10=14,
∴AB=CD=14,
设AE=y,则BE=14-y,
由翻折的性质得,∠AEF=∠A′EF,∠BEC=∠B′EC,
∴∠AEF+∠BEC=90°,
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEC,
又∵∠A=∠B=90°,
∴△AEF∽△BCE,
∴
| AF |
| BE |
| AE |
| BC |
即
| 5 |
| 14-y |
| y |
| 8 |
整理得,y2-14y+40=0,
解得y1=4,y2=10,
由图可知,AE大于AB的一半,
所以AE=10.
故选A.
点评:本题考查了翻折变换的性质,相似三角形的判定与性质,勾股定理的应用,熟记各性质是解题的关键,难点在于多次求三角形相似并利用相似三角形的对应边成比例列出比例式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中是假命题的是( )
| A、同旁内角互补,两直线平行 |
| B、垂线段最短 |
| C、在同一平面内,过一点有且只有一条直线与已知直线垂直 |
| D、直线外一点到这条直线的垂线段叫做点到直线的距离 |
如果等式(
)2=x成立,那么x为( )
| -x |
| A、x≤0 | B、x=0 |
| C、x<0 | D、x≥0 |
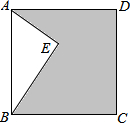 如图,点E在正方形ABCD内,满足∠AEB=90°,AE=5.BE=12,则阴影部分的面积是( )
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=5.BE=12,则阴影部分的面积是( )| A、39 | B、69 |
| C、139 | D、169 |
下列运算正确的是( )
| A、5a-3a=2 |
| B、a2+a2=2a4 |
| C、3a2-2a2=a2 |
| D、-2(a-1)=-2a-1 |
数轴上到表示-2的点距离为4的点所表示的数是( )
| A、1.5 | B、-6 |
| C、1或-6 | D、2或-6 |
 如图,∠A=60°,BD平分∠ABC,CD是△ABC的外角∠ACE的平分线,BD交CD于点D,求∠D的度数.
如图,∠A=60°,BD平分∠ABC,CD是△ABC的外角∠ACE的平分线,BD交CD于点D,求∠D的度数.