题目内容
13.在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,BD=$\frac{9}{5}$,则tanB=$\frac{4}{3}$.分析 利用射影定理可得AD的长,由勾股定理得CD的长,根据题中条件可知∠B=∠DCA,所以把做题方向转化到△ADC中,用正切即可解答.
解答 解:设AD=x,
∵∠ACB=90°,CD⊥AB,
∴AC2=AD•AB,
即42=x(x+$\frac{9}{5}$),
解得:x=-5(舍去),x=$\frac{16}{5}$,
∴CD=$\frac{12}{5}$,
∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD.
∴tanB=tan∠ACD=$\frac{AD}{CD}$=$\frac{\frac{16}{5}}{\frac{12}{5}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 此题主要考查了解直角三角形的能力.关键是找出∠B=∠ACD,会利用三角函数的定义求值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
3.点M(2,-1)向上平移3个单位长度得到的点的坐标是( )
| A. | (2,-4) | B. | (5,-1) | C. | (2,2) | D. | (-1,-1) |
4. 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )| A. | 19° | B. | 29° | C. | 63° | D. | 73° |
1.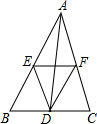 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
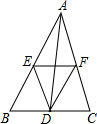 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
18. 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
根据以上图表信息,解答下列问题:
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:学生对使用计算器影响计算能力发展的看法统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数 | 100 | 60 | m |
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
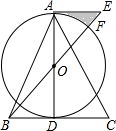 如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.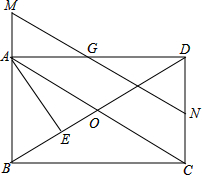 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )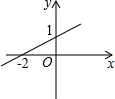 一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.
一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.