Question

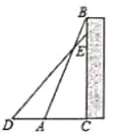
【题目】如图，矩形纸片ABCD中，AB=8，AD=6，折叠纸片使AD边与对角线BD重合，折痕为DG，则线段A'B的长度为____，折痕DG的长度为____．

Answer 1

【答案】4 3．

【解析】

在矩形中根据勾股定理可求出BD的长，由折叠得DA＝DA′＝6，进而求出A′B，在Rt△A′BG中，由勾股定理建立方程可求出A′G，即AG，在Rt△ADG中，由勾股定理可求出DG．

∵矩形纸片ABCD中，AB=8，AD=6，

∴BD10，

由折叠得：DA=DA'=6，GA=GA'，

∴A'B=DB﹣DA'=10﹣6=4，

设GA=GA'=x，则GB=8﹣x，

在Rt△A'BG中，由勾股定理得：x2+42=(8﹣x)2，

解得：x=3，即AG=3，

在Rt△ADG中，由勾股定理得：DG3．

故答案为：4，3．