题目内容
4.如图,已知射线CB∥OA,∠C=∠OAB=100°,(1)求证:OC∥AB.
(2)在射线CB上,E,F为线段CB上两个动点,且在运动过程中始终满足OE平分∠COF,OB平分∠AOF,求∠BOE的度数.
(3)在(2)条件下,在运动过程中,是否存在某种情况使∠OEC=∠OBA?若存在,请求出∠OBA的度数;若不存在说明理由.
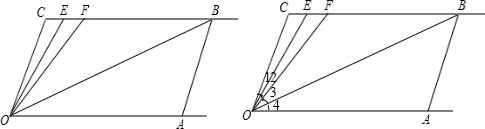
分析 (1)根据CB∥OA,可得∠C与∠OCA的关系,再根据∠C=∠OAB=100°可以解答本题.
(2)根据题目中提供的信息,进行灵活变化,求出各个角之间的关系,从而可以得到∠BPF的度数.
(3)根据第(1)和(2)中得到的结论可以推出∠1、∠2、∠3、∠4之间的关系,从而可以得到∠OBA的度数.
解答 解:(1)∵CB∥OA,
∴∠C+∠COA=180°.
∵∠C=∠OAB=100°,
∴∠COA=80°.
∴∠COA+∠OAB=180°.
∴OC∥AB.
(2)如下图所示:
∵在射线CB上,E,F为线段CB上两个动点,且在运动过程中始终满足OE平分∠COF,OB平分∠AOF,
∴∠1=∠2,∠3=∠4.
∵∠BOE=∠2+∠3=$\frac{1}{2}∠COA$,∠COA=80°,
∴∠BOE=40°.
(3)存在某种情况使∠OEC=∠OBA.
如下图所示:
∵在射线CB上,E,F为线段CB上两个动点,且在运动过程中始终满足OE平分∠COF,OB平分∠AOF,
∴∠1=∠2,∠3=∠4.
∵OC∥AB,∠COB=∠1+∠2+∠3,
∴∠COB=∠OBA,∠OBA=∠1+∠2+∠3.
∵CB∥OA,∠EOA=∠2+∠3+∠4,
∴∠OEC=∠EOA,∠OEC=∠2+∠3+∠4.
∵∠OEC=∠OBA,
∴∠2+∠3+∠4=∠1+∠2+∠3.
∴∠1=∠4.
∵∠1=∠2,∠3=∠4,∠COA=80°,
∴∠1=∠2=∠3=∠4=20°.
∴∠BOC=60°.
∵OC∥AB,
∴∠OBA=∠BOC.
即∠OBA=60°.
点评 本题考查平行线的性质、角的计算,解答本题的关键是理清题目中给出的信息,找出所求问题需要哪些信息.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.下列方程组中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{xy=2}\\{x+y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+y=1}\\{\frac{{x}^{2}}{x}+y=-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{\frac{x}{2}-\frac{y}{4}=1}\end{array}\right.$ |
15.用一个平面去截一个几何体,截面的形状是三角形,那么这个几何体不可能是( )
| A. | 圆锥 | B. | 五棱柱 | C. | 正方体 | D. | 圆柱 |
9.在平行四边形ABCD中,$\overrightarrow{CA}+\overrightarrow{BD}+\overrightarrow{DC}$等于( )
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{BA}$ | D. | $\overrightarrow{BD}$ |
16.李明学习小组在张研究员的带领下,某日在该地的不同高度处同时进行了若干次实验,测得数据如表:
(1)在直角坐标系中作出各组有序数对(h,t)所对应的点;
(2)这些点是否近似的在一条直线上?
(3)写出h与t之间的一个近似关系式;
(4)估计此时3km高度处的温度.
| h(km) | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| t(℃) | 28 | 23.8 | 21.6 | 18.3 | 15 | 11.7 |
(2)这些点是否近似的在一条直线上?
(3)写出h与t之间的一个近似关系式;
(4)估计此时3km高度处的温度.
 如图,已知AB为⊙O的直径,CD⊥AB于点D,交⊙O于点F,AC交⊙O于点E,BE交CD于点G.求证:FD2=CD•GD.
如图,已知AB为⊙O的直径,CD⊥AB于点D,交⊙O于点F,AC交⊙O于点E,BE交CD于点G.求证:FD2=CD•GD. 如图,A(4、4),B(-2,2),C(3,0),
如图,A(4、4),B(-2,2),C(3,0),