Question

【题目】中，，，点为直线上一动点（点不与，重合），以为边在右侧作正方形，连接.

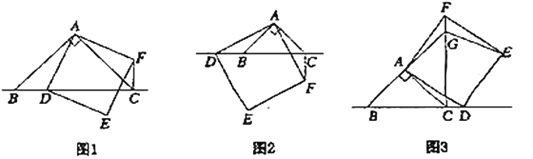
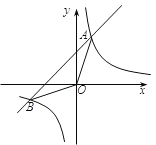
（1）观察猜想：如图1，当点在线段上时，

①与的位置关系为：______.②，，之间的数量关系为：______；（将结论直接写在横线上）

（2）数学思考：如图2，当点在线段的延长线上时，（1）中的结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.

（3）拓展延伸：如图3，当点在线段的延长线上时，延长交于点，连接.若已知，，请直接写出的长.

Answer 1

【答案】观察猜想：（1）①； ②；数学思考：（2）结论①仍然成立，见解析，结论②变为，见解析；拓展延伸：（3）.

【解析】

（1）根据正方形的性质证明△DAB≌△FAC，根据全等三角形的性质即可得到结论；

（2）根据正方形的性质证明△DAB≌△FAC，再根据等腰直角三角形的性质即可求解；

（3）分别过点、作垂线，根据（1）（2）的结论，再证明，根据勾股定理即可求解.

解：（1）在正方形ADEF中，AD=AF,

∵∠BAC=∠DAF=90°，

∴∠BAD=∠CAF，故△DAB≌△FAC

∴∠B=∠ACF，∴∠ACB+∠ACF=90°，即

②∵△DAB≌△FAC

∴CF=BD,

∵BC=BD+CD，

∴BC=CF+CD

（2）结论①仍然成立，结论②变为.

证明：∵四边形是正方形，

∴，，

∵，

∴，

∴.

又，

∴.

∴，，

∵，

∴.

设与交于点，则，

在中，，

∴，

∴即

（3）分别过点、作垂线，类比（1）（2）结论可知，，，

又AD=DE,∠AND=∠DHE=90°，

∵∠NAD+∠ADN=90°，∠EDH+∠ADN=90°，

∴∠NAD=∠EDH

∴

∴，，，，

由勾股定理得