题目内容
3. “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h(约为19.4m/s).如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方40m的C处(即AC=40m),过了2s后,行驶到B处,测得小汽车与车速检测仪间距离AB为50m,问:这辆小汽车超速了吗?
分析 本题求小汽车是否超速,其实就是求BC的距离,直角三角形ABC中,有斜边AB的长,有直角边AC的长,那么BC的长就很容易求得,根据小汽车用2s行驶的路程为BC,那么可求出小汽车的速度,然后再判断是否超速了.
解答 解:在Rt△ABC中,AC=40m,AB=50m;
据勾股定理可得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{5{0}^{2}-4{0}^{2}}$=30(m)
小汽车的速度为v=$\frac{30}{2}$=15(m/s),
∵15m/s<19.4m/s;
∴这辆小汽车没有超速行驶.
答:这辆小汽车没有超速了.
点评 此题主要考查了勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,根据示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
13.-(-a+b-1)去括号结果正确的是( )
| A. | -a+b-1 | B. | a-b+1 | C. | -a+b+1 | D. | a+b+1 |
14.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )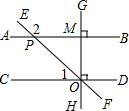

| A. | 130° | B. | 138° | C. | 140° | D. | 142° |
11.-8的立方根是( )
| A. | -2$\sqrt{2}$ | B. | ±2 | C. | 2 | D. | -2 |
15.若a,b(a<b)是关于x的方程x-(x-m)(x-n)=0的两根,且m<0<n,则a,b,m,n的大小关系是( )
| A. | m<a<b<n | B. | a<m<n<b | C. | a<m<b<n | D. | m<a<n<b |
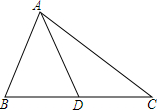 △ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.
△ABC中,AB=AD,∠C=45°,AC=m,则BC+CD=$\sqrt{2}$m.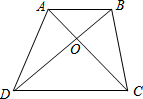 如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.
如图,梯形ABCD中,AB∥CD,AB=2,CD=3,若S△AOB=1,则S梯形ABCD=$\frac{25}{4}$.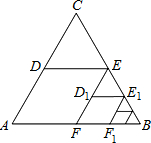 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.