题目内容
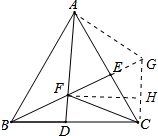
 如图,在等边△ABC中,BD=CE,BE交AD于点F.若BF=3,AF=4,则CF=
如图,在等边△ABC中,BD=CE,BE交AD于点F.若BF=3,AF=4,则CF=考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:延长FE至点G,使FG=AF,连接AG、CG,作FH⊥CG于H,先证△ABD≌△BCE,得出∠BAD=∠CBE,再证明△AFG是等边三角形,得出FG=4,然后证明△ACG≌△ABF,得出CG=BF=3,∠FGC=60°,求出GH=
FG=2,FH=2
,CH=CG-GH=1,即可求出CF=
.
| 1 |
| 2 |
| 3 |
| 13 |
解答:解:延长FE至点G,使FG=AF,连接AG、CG,作FH⊥CG于H,如图所示:
 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴∠ABC=∠BCA=∠BAC=60°,AB=BC,
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=60°,
∵FG=AF,
∴△AFG是等边三角形,
∴FG=AF=AG=4,∠FAG=∠AGF=60°,
∴∠CAG=∠BAF,
∴△ACG≌△ABF(SAS),
∴CG=BF=3,
∵∠CAG+∠ACG=∠BAD+∠ABF=60°,
∴∠AGC=120°,
∴∠FGC=60°,
∵FH⊥CG,
∴∠GFH=30°,
∴GH=
FG=2,FH=2
,
∴CH=CG-GH=1,
∴CF2=CH2+FH2=12+(2
)2=13,
∴CF=
;
故答案为:
.
 ∵△ABC是等边三角形,
∵△ABC是等边三角形,∴∠ABC=∠BCA=∠BAC=60°,AB=BC,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=60°,
∵FG=AF,
∴△AFG是等边三角形,
∴FG=AF=AG=4,∠FAG=∠AGF=60°,
∴∠CAG=∠BAF,
∴△ACG≌△ABF(SAS),
∴CG=BF=3,
∵∠CAG+∠ACG=∠BAD+∠ABF=60°,
∴∠AGC=120°,
∴∠FGC=60°,
∵FH⊥CG,
∴∠GFH=30°,
∴GH=
| 1 |
| 2 |
| 3 |
∴CH=CG-GH=1,
∴CF2=CH2+FH2=12+(2
| 3 |
∴CF=
| 13 |
故答案为:
| 13 |
点评:本题考查了全等三角形的判定与性质、等边三角形的性质与判定以及勾股定理的运用;本题难度较大,通过作辅助线构造等边三角形,证明三角形全等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若一元二次方程2x2+2x+m=0有一个实数解x=1,则m的取值是( )
| A、m=-4 | ||
| B、m=1 | ||
| C、m=4 | ||
D、m=
|
 如图,在△ABC中,D为BC上一点,且∠B=∠C=∠BAD,∠ADC=∠CAD.求∠BAD的度数.
如图,在△ABC中,D为BC上一点,且∠B=∠C=∠BAD,∠ADC=∠CAD.求∠BAD的度数. 在△ABC中,AB=8,BC=6,AC=7,AE,AD分别为BC边上的中线和高,求DE的长.
在△ABC中,AB=8,BC=6,AC=7,AE,AD分别为BC边上的中线和高,求DE的长. 如图,直线AB、CD相交于点O,若∠COE=72°,OA平分∠COE,则∠DOB=
如图,直线AB、CD相交于点O,若∠COE=72°,OA平分∠COE,则∠DOB=