题目内容
15.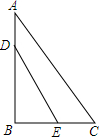 如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.
如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.
分析 △ABC的面积=$\frac{1}{2}$×3×4=6,设BE为x,由线段DE平分△ABC的面积得出BD=$\frac{6}{x}$,根据平分△ABC的周长建立方程求得方程的解即可.
解答 解:存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.
理由:△ABC的面积=$\frac{1}{2}$×3×4=6,
设BE为x,由题意得
x+$\frac{6}{x}$=$\frac{1}{2}$×(3+4+5)
解得:x1=3+$\sqrt{3}$(BC=3,不合题意,舍去),x2=3-$\sqrt{3}$,
则BD=$\frac{6}{x}$=3+$\sqrt{3}$,
所以当DE=3-$\sqrt{3}$,BD=3+$\sqrt{3}$线段DE既平分△ABC的面积又平分△ABC的周长.
点评 此题考查一元二次方程的实际运用,掌握三角形的面积与周长计算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
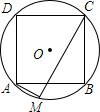 如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长.
如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长. 如图,菱形ABCD中,BD=24,AC=10,则该菱形的周长为52.
如图,菱形ABCD中,BD=24,AC=10,则该菱形的周长为52.