题目内容
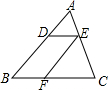如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，DE∥BC，EF∥AB，且S△ABC=4，S△ADC=9．（1）求证：△ADE∽△EFC；
（2）若△ADE的周长为20，求△ABC的周长．
考点：相似三角形的判定与性质
专题：
分析：（1）由DE∥BC，EF∥AB，得出△ADE∽△ABC，△EFC∽△ABC，证出△ADE∽△EFC；
（2）根据相似三角形面积的比等于相似比，求出相似比，再根据周长的比等于相似比求出△ABC的周长．
（2）根据相似三角形面积的比等于相似比，求出相似比，再根据周长的比等于相似比求出△ABC的周长．
解答：（1）证明：∵DE∥BC，EF∥AB，
∴△ADE∽△ABC，△EFC∽△ABC，
∴△ADE∽△EFC；
（2）解：∵△ADE∽△ABC，
∴
=
，
=(
)2=
，
∴
=
=
，
∵AD+DE+AE=20，
∴AB+BC+AC=30．
∴△ADE∽△ABC，△EFC∽△ABC，
∴△ADE∽△EFC；
（2）解：∵△ADE∽△ABC，
∴
| AD+DE+AE |
| AB+BC+AC |
| AD |
| AB |
| S△ADE |
| S△ABC |
| AD |
| AB |
| 4 |
| 9 |
∴
| AD+DE+AE |
| AB+BC+AC |
| AD |
| BC |
| 2 |
| 3 |
∵AD+DE+AE=20，
∴AB+BC+AC=30．
点评：本题考查了相似三角形的判定与性质；关键是证明三角形相似．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图，△ABC中，点D在AB边上，∠A=∠1，∠B=∠2，则△ABC的形状是（ ）| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
如图用圆心角为120°，半径为6的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的高是（ ）| A、6 | ||
| B、8 | ||
C、3
| ||
D、4
|