题目内容
 已知反比例函数y1=
已知反比例函数y1=| k |
| x |
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)在x轴的正半轴上存在一点P,且△ABP的面积是6,请直接写出点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据一次函数图象在上方的部分是不等式的解,可得答案;
(3)根据面积的和差,可得答案.
(2)根据一次函数图象在上方的部分是不等式的解,可得答案;
(3)根据面积的和差,可得答案.
解答:解:(1)∵函数y1=
的图象过点A(1,4),即4=
,
∴k=4,即y1=
,
又∵点B(m,-2)在y1=
上,
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即
,
解之得
.
∴y2=2x+2.
 反比例函数的解析式为y1=
反比例函数的解析式为y1=
,
一次函数的解析式为 y2=2x+2;
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴-2<x<0或x>1;
(3)如图,直线AB与x轴交点C的坐标(-1,0),
∴S△ABP=S△APC+S△BPC=
PC×4+
PC×|-2|=
PC×6=6.
∴PC=2
∴P的坐标(1,0).
| k |
| x |
| k |
| 1 |
∴k=4,即y1=
| 4 |
| x |
又∵点B(m,-2)在y1=
| 4 |
| x |
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即
|
解之得
|
∴y2=2x+2.
 反比例函数的解析式为y1=
反比例函数的解析式为y1=| 4 |
| x |
一次函数的解析式为 y2=2x+2;
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴-2<x<0或x>1;
(3)如图,直线AB与x轴交点C的坐标(-1,0),
∴S△ABP=S△APC+S△BPC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PC=2
∴P的坐标(1,0).
点评:本题考查了反比例函数与一次函数的交点问题,利用待定系数法求解析式,函数与不等式的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a为实数,则
-a
的化简结果正确的是( )
| -a3 |
-
|
A、(-a+1)
| ||
B、(a+1)
| ||
C、(a-1)
| ||
| D、0 |
2013年黄石市旅游收入达52644.85万元,比2010年增长了40.7%,用科学记数法表示2013年黄石市旅游收入是( )元(保留三个有效数字)
| A、526×102 |
| B、5.26×104 |
| C、526×106 |
| D、5.26×108 |
 如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为
如图,△ABC内接于⊙O,∠OAB=20°,则∠C的度数为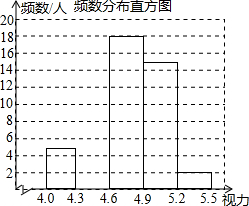 为了了解学生的视力情况,某中学对该校学生进行一次视力抽样调查,根据抽样调查的情况,绘制成如下统计图表(不完整):
为了了解学生的视力情况,某中学对该校学生进行一次视力抽样调查,根据抽样调查的情况,绘制成如下统计图表(不完整): 如图,已知二次函数y=a(x-h)2+
如图,已知二次函数y=a(x-h)2+