题目内容
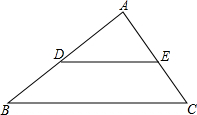如图所示，已知△ABC中，DE∥BC，AD=8，AC=6，BD=AE，求BD的长．考点：平行线分线段成比例
专题：计算题
分析：根据平行线分线段成比例定理，由DE∥BC得
=
，而BD=AE，则CE=AC-BD=6-BD，所以
=
，再利用比例的性质得到BD2+8BD-48=0，然后解此一元二次方程即可得到BD的长．
| AD |
| BD |
| AE |
| CE |
| 8 |
| BD |
| BD |
| 6-BD |
解答：解：∵DE∥BC，
∴
=
，
∵AD=8，AC=6，BD=AE，
∴CE=AC-BD=6-BD，
∴
=
，
整理得BD2+8BD-48=0，解得BD=4或BD=-12（舍去），
∴BD的长为4．
∴
| AD |
| BD |
| AE |
| CE |
∵AD=8，AC=6，BD=AE，
∴CE=AC-BD=6-BD，
∴
| 8 |
| BD |
| BD |
| 6-BD |
整理得BD2+8BD-48=0，解得BD=4或BD=-12（舍去），
∴BD的长为4．
点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．也考查了比例的性质．
练习册系列答案
名校课堂系列答案
相关题目
在-
，-2，
，
，3.14，（
）0中无理数的个数是（ ）
| π |
| 3 |
| 4 |
| ||
| 2 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，AB是⊙O的直径，AM，BN分别切⊙O于点A，B，CD交AM，BN于点D，C，DO平分∠ADC．
如图，已知⊙O的半径为4，弦BC长为4